Расчет переходных процессов в электрических цепях классическим методом

1. Составляют систему дифференциальных уравнений по законам Кирхгофа.

2. Записывают общее решение дифференциального уравнения в виде суммы частного решения неоднородного уравнения – установившийся (принужденный) режим и общего решения однородного уравнения – свободный процесс

или .

3. Рассчитывают принужденные (установившиеся) составляющие токов и напряжений от действия внешних источников ЭДС и источников тока.

4. При определении вида свободной составляющей переходных токов и напряжений составляют и решают характеристическое уравнение. Для этого записывают комплексное сопротивление цепи 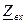, заменяют на и приравнивают к нулю. Решая уравнение , находят корни характеристического уравнения . При одном корне свободные составляющие тока и напряжения имеет вид:

,

.

5. Определяют постоянную интегрирования из начальных условий, т.е. при .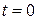

, ;

, .

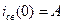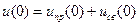Следует помнить, что корень характеристического уравнения всегда отрицателен, т.к. свободный процесс – процесс затухающий, он обусловлен запасом энергии в реактивных элементах электрической цепи.

При анализе переходных процессов вводят понятие постоянной времени цепи .

Пример. Последовательная 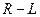цепь подключается к источнику постоянной ЭДС В (рис.4.4), Ом, мГн. Определить и .

Рис.4.4.

Решение. Цепь содержит один реактивный элемент и описывается дифференциальным уравнением первой степени:

.

Решение уравнения имеет вид .

Находим . В установившемся режиме индуктивность не оказывает сопротивления постоянному току, следовательно

А.

Составляем характеристическое уравнение и находим его корень:

,

,

.

Тогда

.

Определяем 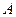из начальных условий:

.

По первому закону коммутации:

,

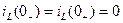тогда при :

,

отсюда

.

Ток в цепи (рис.6.7).

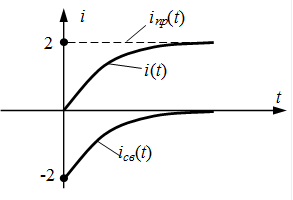
Рис.4.5.

Напряжение на индуктивности (рис.4.4).

Рис.4.6.

Пример. Используя условие предыдущей задачи определить время через которое ток в цепи достигнет значения .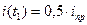

Решение.

, А;

, ,

,

с.

Пример. Определить постоянную времени цепи (рис.4.7).

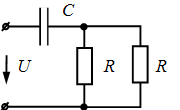
Рис.4.7.

Решение. Составляем характеристическое уравнение , приравниваем к нулю и находим корень характеристического уравнения:

.

Постоянная времени , следовательно, .

Дата добавления: 2015-08-27