|
Читайте также: |
В цепях электросвязи, электронных и полупроводниковых устройств используются периодические несинусоидальные токи и напряжения, т.е. сигналы, изменяющиеся во времени по периодическому несинусоидальному закону (рис.4.8).
Рис.4.8. Несинусоидальные сигналы.
Из математики известно, что несинусоидальная периодическая функция может быть представлена в виде гармонического ряда Фурье:
,
где 
– постоянная составляющая,
– амплитуда синусоидальной составляющей k ‑ ой гармоники,
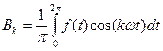– амплитуда косинусной составляющей k ‑ ой гармоники.
Существует вторая форма записи ряда Фурье:
,
где 
, 
.
Пример разложения в ряд Фурье сигналов, изображенных на рис 4.8:
Последовательность прямоугольных импульсов:
;
Последовательность треугольных импульсов:
.
Гармоника, частота которой равна частоте несинусоидальной периодической функции, называется основной. Остальные гармоники – высшие.
Действующее значение несинусоидальных токов и напряжений – это величины, измеряемые амперметром и вольтметром.
Действующее значение периодической функции тока и напряжения, представленной рядом Фурье, определяется через действующие значения всех гармоник:
,
.
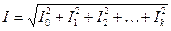Пример. Напряжение источника ЭДС задано в виде ряда Фурье:
В.
Вольтметр электромагнитной системы, подключенный к источнику, покажет действующее значение напряжения:
В.
Дата добавления: 2015-08-27; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Расчет переходных процессов в электрических цепях классическим методом | | | Мощность в линейных электрических цепях с негармоническими напряжениями и токами |