Правила перевода числа из 10-ой системы в систему с основанием S ( (10)®(S) ).

Тема 4: Арифметические основы ЭВМ. Основные понятия.

Системой счисления называют способ представления (т.е. записи) чисел с помощью некоторого алфавита символов, которые принято называть цифрами. Различают позиционные и непозиционные системы счисления. В позиционной системе значение цифры зависит от ее позиции в записи числа, а в непозиционной – не зависит. Например, в привычной нам десятичной системе (в которой используется 10 арабских цифр от 0 до 9) крайняя справа цифра в записи числа обозначает количество единиц, следующая цифра слева – количество десятков, следующая – количество сотен и т.д. Рассмотрим конкретное число: 35257=30000+5000+200+50+7. В данном примере в записи числа два раза используется цифра 5, но она задает различные значения в зависимости от своей позиции в числе. Примером непозиционной системы может служить Римская система.

Любая позиционная система характеризуется своим основанием и базой. Основанием системы счисления называют количество цифр, используемых для записи чисел в этой системе, а базой называют набор (алфавит) цифр, используемых в этой системе. Если обозначить основание системы счисления как S, тогда база этой системы должна состоять из следующих цифр: 0, 1, …, S-1. Тогда запись любого числа X в системе с основанием S может быть представлена в виде полинома от основания S:

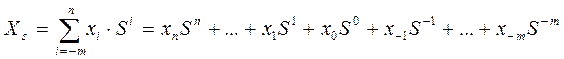
где X_i – цифры, используемые для записи числа,

i – номер позиции (разряда) цифры в числе (разряды нумеруются влево и вправо от запятой).

n – номер самого старшего разряда в числе,

-m – номер самого младшего разряда в числе.

Данный способ записи числа принято называть полной формой, однако мы привыкли пользовать краткой формой записи, когда записываются только цифры числа (коэффициенты полинома X_i).

X_(S) = X_nX_n-1...X₁X₀ , X_-1X_-2...X_-m.

Запишем в полной и краткой форме конкретное десятичное число (S=10):

X₍₁₀₎ = 2×10³+5×10²+0×10¹+6×10⁰+9×10^-1+6×10^-2+1×10^-3 - полная форма

X₍₁₀₎ = 2506,961 - краткая форма

В ЭВМ получили применение только позиционные системы счисления, причем с основаниями кратными двум: 2-ая, 8-ая, 16-ая.

Название системы счисления	Основание S	База системы счисления	Примеры чисел
Десятичная		0,1,2,3,4,5,6,7,8,9	45798,389; 7778932,9998
Двоичная		0,1	1111101,11; 100001110,101
Восьмеричная	8=2^3	0,1,2,3,4,5,6,7	456716,7723; 2651127,3462
Шестнадцатиричная	16=2^4	0,1,2,3,4,5,6,7,8,9, A,B,C,D,E,F	356,76899; A67,2; FC41,2 7B45A,EC; ACE27,C2AA3

Правила перевода числа из 10-ой системы в систему с основанием S ((10)®(S)).

1. Правило перевода целого десятичного числа в систему с основанием S.

Необходимо последовательно делить вначале само число, а затем получаемые от деления частные на основание S. Причем выполняется целочисленное деление, т.е. с нахождением остатка от деления. Деление частных выполняется до тех пор, пока не будет получено частное меньше основания S. Частное от последнего деления записывается как старшая цифра в записи числа в системе S. В качестве остальных цифр числа берутся остатки от остальных делений, записанные с конца (т.е. в обратном направлении относительно выполненных делений).

Решить примеры: 1) X₁₀=72; (10)®(2). 2) X₁₀=342; (10)®(8). 3) X₁₀=859; (10)®(16).

2. Правило перевода десятичной правильной дроби в систему с основанием S.

Необходимо последовательно умножать вначале исходную дробь, а затем дробные части получающихся произведений на основание S. Умножение выполняется до тех пор, пока не будет получено произведение с нулевой дробной частью (целое число). В качестве цифр искомой дроби в системе с основанием S записываются целые части от полученных произведений в прямом порядке (т.е. в соответствии с порядком выполненных умножений).

Решить примеры: 1) X₁₀=0,1875; (10)®(2). 2) X₁₀=0,87; (10)®(8). 3) X₁₀=0,48; (10)®(16).

3. Перевод неправильной десятичной дроби в систему с основанием S.

Необходимо взять отдельно целую и дробную (как правильную дробь) части числа, выполнить их перевод согласно правилам 1. и 2. соответственно, а затем соединить полученные результаты.

Пример: Х₁₀=24,375; (10)®(2). 24₁₀=11000₂; 0,375₁₀=0,011₂ Þ X₂=11000,011.

Дата добавления: 2015-08-27