Orthogonal transformations of plane

A regular square matrix 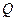for which is called orthogonal.

Theorem 10. For an orthogonal matrix .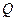

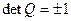Proof. Multiplying the equality consecutively on the right and left on 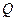we obtain the following: 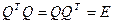. Then since: a) the determinant of product of square matrices of the same order is equal to product of the determinants of multipliers; b) the determinant of a matrix does changes at its transposition; c) . ÿ

Theorem 11. An orthogonal matrix of the second order 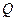for which can be represented as where 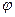is some number, and an orthogonal matrix with can be represented as .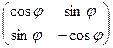

An orthogonal transformation of plane 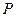is a linear operator 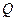of the form 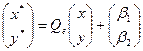of which the matrix 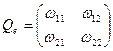is orthogonal in any orthonormal system of coordinates.

Theorem 12. An orthogonal transformation preserves: 1) the distance between any pair of points;

2) angles between lines:

3) scalar product of vectors.

Proof. 1. Let an orthogonal transformation 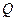of the form 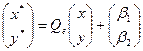transferring a pair of points to a pair of points respectively. Then .

By Theorem 11 the matrix of an orthogonal transformation 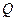in an orthonormal system of coordinates has the form: . Therefore the coordinates of images and pre-images of the considered pairs will be connected by 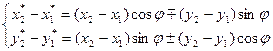. Then using these expressions we find that the distances between images and between pre-images are equal. In fact,

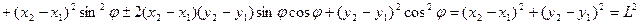
2. From preserving the distance between every pair of points at an orthogonal transformation follows preserving values of angles between lines on plane since in this case every triangle transfers to equal itself.

3. If at an orthogonal transformation lengths of vectors and values of angles between them are preserved then scalar product of every pair of vectors on plane will be preserved. ÿ

Дата добавления: 2015-08-27