Affine transformations and their properties

L E C T U R E 6

An operator 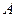mapping a plane (or just a mapping of plane) 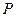on a plane 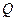is a rule by which every point of plane 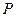is put a unique point of the plane 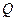. A mapping is denoted as follows: 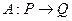. If a point 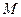of a plane 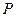is transferred to a point 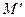of a plane 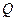, we denote this by , and 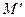is the image of 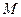, 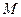is a pre-image of .

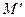A mapping 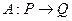is a bijection ( or bijective) if every point of the plane 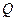has a unique pre-image. A mapping that is inverse to a bijective mapping 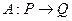is the mapping 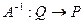such that for every point 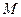of the plane 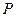the following holds: 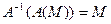. A mapping 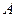of plane 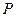to itself is called a transformation of the plane 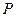. A consecutive realization of transformations 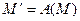and 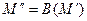is called the product (or composition) of these transformations. The product of operators is written as .

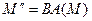A point of a plane 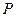transferred by a transformation 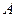to itself is called a fixed (immovable) point for 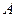. A set of the plane 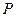consisting of fixed points for 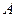is called fixed for 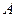. A set of points of 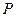transferred by 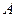to itself is called an invariant set of the transformation .

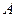Let in a plane with Cartesian system of coordinates 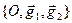every its point 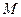be put a unique point 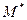, i.e. a transformation of the plane be given. Let radius-vectors of these points be 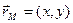and 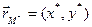. Then the coordinates 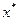and 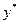are some functions of 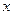and .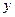

An operator 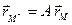is linear if in every Cartesian system of coordinates 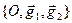it is given by the formulas: .

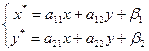A linear operator can be written in matrix form: 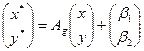where 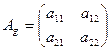is the matrix of the linear operator 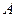in the Cartesian system of coordinates .

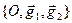A linear operator 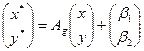mapping a plane to itself with matrix 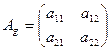for which in every basis 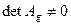is called an affine transformation of the plane.

Theorem 1. If a linear transformation has regular matrix in some Cartesian system of coordinates then the matrix of this transformation will be regular in any other Cartesian systems of coordinates.

Theorem 2. Every affine transformation has the inverse transformation that is unique.

Proof. Since 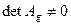, the system of linear equations 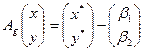has a unique solution 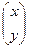for every vector 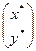. It means that for every image of an affine transformation there is a unique pre-image, i.e. there is the inverse transformation. ÿ

Theorem 3. For an affine transformation the image of a straight line is a straight line.

Proof. Let a lin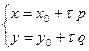e where 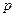and 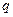are non-simultaneously equal to zero coordinates of directing vector of the line and an affine transformation 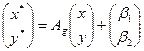be given. Then the image of the line will be the set of points of the plane with coordinates

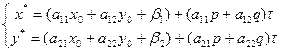since .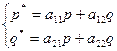

Observe that if 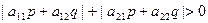then we have a line.

Assume the contrary: let 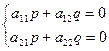. Since the transformation is affine, 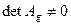and consequently 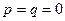is a unique solution of this system of equations, contradicting our hypothesis. ÿ

Theorem 4. For an affine transformation the image of parallel lines are parallel lines, and the point of intersecting the lines-pre-images transfers to the point of intersecting their images.

Proof. Suppose that a pair of parallel lines was transferred by an affine transformation to intersecting or coinciding lines. Consider one of points that are common for the images of lines. Since every affine transformation is bijective, the pre-image of common point is unique and must belong simultaneously to each of the lines-pre-images. However there are no such points since the lines-pre-images are parallel. Consequently, the images of parallel lines are also parallel. If the lines-pre-images are intersected then since every affine transformation is bijective, the image of their point of intersecting can be only the point of intersecting of the images of these lines. ÿ

Theorem 5. For an affine transformation dividing a segment in a given ratio is preserved.

Proof. Let 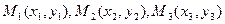be points lying on some line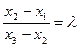, and and 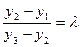where 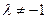. Let 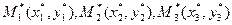be their images at an affine transformation 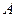. It needs to show that 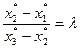and .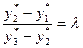

Let 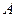be given in the form: 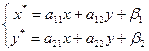. Then

.

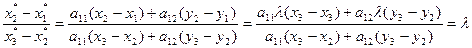It is showed analogously that 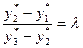. Observe that from the obtained equalities follow equality of ratio of lengths of images and ratio of lengths of pre-images of segments lying on one line: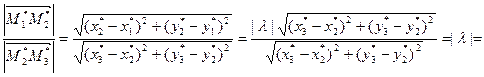

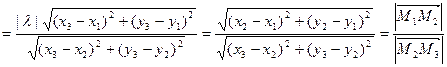. ÿ

Observe also that Theorem 5 implies that at an affine transformation a segment of a line transfers to a segment.

Theorem 6. For an affine transformation the ratio of lengths of images of two segments lying on parallel lines is equal to the ratio of lengths of their pre-images.

Proof. Let 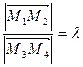. Draw a line 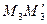that is parallel to .

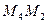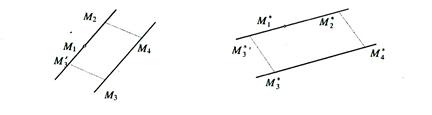
Since at an affine transformation images of parallel lines are parallel, by Theorem 4 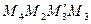and 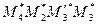are parallelograms. Consequently, 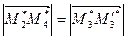. At last by Theorem 5 we obtain: 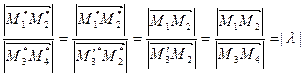. ÿ

To clarify geometric sense of module and sign of the determinant of a matrix of some affine transformation we give another definition of orientation of pair of non-collinear vectors on plane, transferring consideration of this plane to the space. Let 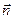be its some fixed normal vector directed to the direction of an observer. A pair of non-collinear vectors 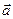and 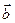is right (left) oriented if there is 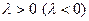such that .

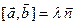Theorem 7. 1) At an affine transformation the ratio of the area of the image of parallelogram to the area of the parallelogram itself is equal to the absolute value of .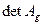

2) At an affine transformation the orientation of the images of a pair of vectors coincides with the orientation of the pre-images if 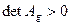and is replaced on opposite if .

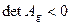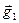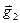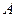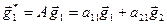Proof. Consider some basis formed by vectors and of which the images at an affine transformation are and 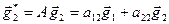respectively. The coefficients 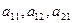and 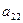are elements of the matrix of linear operator 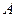, i.e. 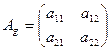. By properties of vector product the area of parallelogram constructed on basis vectors 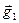and 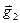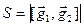, and the area of parallelogram constructed on the images of basis vectors 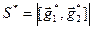. We have:

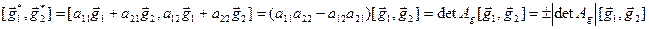Then 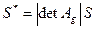, and the orientation of the pair of vectors 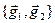is not changed at 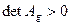and is replaced on opposite at 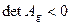. ÿ

Theorem 8. At an affine transformation every Cartesian system of coordinates transfers to a Cartesian system of coordinates, and the coordinates of the image of every point of plane in new system of coordinates will coincide with the coordinates of the pre-image in the original system.

Proof.

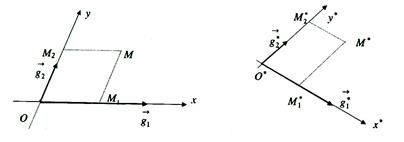
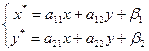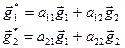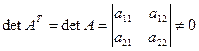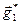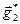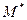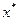At an affine transformation a basis transfers to a basis. Indeed, let the formulas of a transformation be . Then the images of old basis vectors are the vectors . Since , the vectors and are linearly independent, and consequently we can form a basis. Let in new system the coordinates of be and 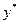. Then by Theorem 5 the following holds:

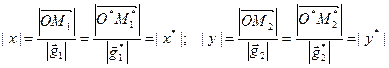. ÿ

Theorem 9. For every curve of the second order that is not an empty set its type cannot be changed at an affine transformation.

Proof. By Theorem 4 and 6 a parallelogram with its interior transfers to a parallelogram, and consequently, a restricted curve transfers to a restricted one. This implies that ellipses and points can transfer only to ellipses and points. On other hand, a point cannot transfer to an ellipse and conversely since every affine transformation is bijective.

Only hyperbolas and parallel lines among curves of the second order have non-connected branches, i.e. there is a line non-intersecting a curve of the second order such that the branches of this curve are located on different sides from the line. This property is obviously preserved at an affine transformation. Parallel lines cannot transfer to branches of a hyperbola by Theorem 4.

Only parabola among non-straight curves of the second order is a unrestricted connected curve. Consequently, a parabola at an affine transformation can transfer only to a parabola.

If a curve of the second order is a point, a line or a pair of parallel or intersecting lines then by Theorems 3 and 4 follows that their type cannot be changed. ÿ

Дата добавления: 2015-08-27