Читайте также:
|
Рассмотрим процесс накопления денежных средств на примере банковских депозитов. Если по условию договора проценты выплачиваются непосредственно инвестору, а не прибавляются к исходной сумме вложения, то такой вариант называется размещением средств под простой процент. Если проценты прибавляются к исходной сумме в конце каждого периода времени (например, года), то такой метод начисления процентов называется сложным процентом. Далее будет рассматриваться только использование сложного процента.
Пусть начисление процентов (капитализация) выполняется в конце каждого года. Тогда в конце первого года наращенная сумма составит 
где S – наращенная сумма; P – начальный капитал, положенный в банк; r – годовая процентная ставка банка.
Если эта сумма (S) остается в банке, то в конце следующего года наращенная сумма составит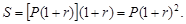 
В общем случае сумма, наращенная за n лет, рассчитывается по формуле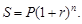 
В течение года проценты могут начисляться несколько раз, тогда наращенная сумма будет увеличиваться. Время между двумя последовательными начислениями процента называется периодом капитализации процента.
Пусть по условию договора с банком годовая процентная ставка составляет r, а проценты капитализируются m раз в течение года. Эффективной процентной ставкой банка для периода капитализации называется процент, нарастающий в течение одного периода капитализации, который определяется по формуле r 
=r/m
Если срок депозита составляет l периодов капитализации, то формулу вычисления наращенной суммы можно обобщить следующим образом: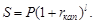 
Процесс нахождения текущей стоимости называется дисконтированием.
Дата добавления: 2015-08-26; просмотров: 69 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Постановка и классификация задач математического программирования. | | | Анализ инвестиционных проектов. |