Постановка и классификация задач математического программирования.

Задачи математического программирования – это задачи определения наилучшего решения из множества допустимых.

В общем виде постановка задачи математического программирования состоит в определении значений переменных х ₁, х ₂, …, х_n, при которых достигается максимум или минимум функции 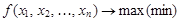(15) при следующих условиях:

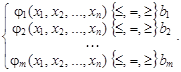
Функция (15) называется целевой функцией, а условия (16) – ограничениями данной задачи. Запись 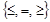в ограничениях означает, что возможен один из знаков £, = или ³. В данной задаче n обозначает число переменных, а m – число ограничений.

Переменные задачи х ₁, х ₂, …, х_n могут иметь различный экономический смысл.

Целевая функция в математическом виде выражает критерий оптимальности, т. е. служит для выбора наилучшего решения. Если используется максимизируемый критерий оптимальности, то целевая функция стремится к максимуму. Если же в качестве критерия оптимальности выступают затраты, то целевая функция стремится к минимуму.

В зависимости от характера целевой функции f и функций ограничений j₁, j₂, ¼, j _m говорят о различных видах задач математического программирования:

· Если целевая функция задачи имеет линейный вид, а ограничения заданы в виде линейных уравнений или неравенств, то это задача линейного программирования. (5 х ₁ + 6 х ₂.)

· Если целевая функция и (или) ограничения содержат нелинейные функции, то это задача нелинейного программирования. (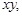 х ², 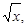sin x)

· Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования.

· Если в задаче математического программирования необходимо учитывать фактор времени, то такая задача является задачей динамического программирования.

Задача линейного программирования. Понятия допустимого и оптимального плана.

задача линейного программирования заключается в том, чтобы найти значения переменных х ₁, х ₂, …, х_n, доставляющие оптимальное значение целевой функции 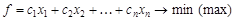при выполнении ограничений (17)

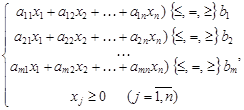где а_ij, b_i, c_j – заданные постоянные величины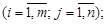

m – число уравнений; n – число переменных.

Ограничения 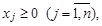с матем.точки зрения - необязательными, но в моделях экономических задач они всегда присутствуют.

Ограничения (17) определяют область допустимых решений.

Набор значений переменных х ₁, х ₂,…, х_n, при котором выполняются все ограничения, называется допустимым решением, или планом. Допустимое решение, при котором функция f принимает максимальное или минимальное значение, называется оптимальным.

Для решения задач линейного программирования необходимо составить математическую модель задачи.

Для решения задач линейного программирования используется симплекс-метод. Автоматизировать решение этим методом можно с помощью надстройки Поиск решения пакета MS Excel.

В случае двух переменных задача линейного программирования может быть решена графическим методом, для автоматизации используется MathCad.

Дата добавления: 2015-08-26