
Читайте также:
|
1. Образование головной преломленной волны. Как отмечалось выше (см. 10.1.4), при критическом угле падения  , когда угол преломления \beta равен 90
, когда угол преломления \beta равен 90  , вдоль границы начнет скользить преломленная волна, которая возникает при
, вдоль границы начнет скользить преломленная волна, которая возникает при  , так как
, так как 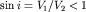 .
.
При падении прямой сферической волны под критическим углом  в точке
в точке 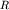 (рис. 4.6) образуются две волны: одна отраженная, движущаяся по лучу
(рис. 4.6) образуются две волны: одна отраженная, движущаяся по лучу  со скоростью
со скоростью 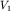 , и вторая, скользящая вдоль границы раздела со скоростью
, и вторая, скользящая вдоль границы раздела со скоростью 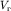 (
(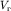 , как правило, равно
, как правило, равно 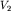 ). Чтобы показать, как эта скользящая преломленная волна выходит на линию наблюдений (ось
). Чтобы показать, как эта скользящая преломленная волна выходит на линию наблюдений (ось  ), воспользуемся принципом Гюйгенса.
), воспользуемся принципом Гюйгенса.
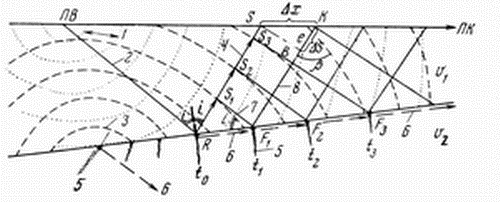
|
| Рис. 4.6. Природа образования сейсмических волн: 1, 2 - фронт и луч прямой волны; 3, 4 - фронт и луч отраженной волны; 5, 6 - фронт и луч преломленной проходящей волны; 7, 8 - фронт и луч головной преломленной волны |
Согласно принципу Гюйгенса, любая точка фронта волны является источником колебаний. В частности, из точки 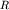 начнет распространяться фронт отраженной волны со скоростью
начнет распространяться фронт отраженной волны со скоростью 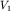 , который через время
, который через время 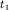 после начала отражения достигнет точки
после начала отражения достигнет точки 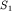 . За это же время в среде
. За это же время в среде 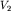 фронт проходящей преломленной волны, перпендикулярный границе раздела, достигнет точки
фронт проходящей преломленной волны, перпендикулярный границе раздела, достигнет точки  . Соответственно за время
. Соответственно за время 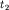 фронты этих волн достигнут точек
фронты этих волн достигнут точек 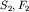 , за время
, за время  и так далее. Поскольку
и так далее. Поскольку  , преломленная волна распространяется быстрее отраженной.
, преломленная волна распространяется быстрее отраженной.
Фронт проходящей преломленной волны, скользя вдоль границы раздела, возбуждает в верхнем слое колебания, которые и вызывают появление так называемой головной преломленной волны. В самом деле, за время 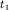 , область возмущений в верхней среде будет заключена в треугольнике
, область возмущений в верхней среде будет заключена в треугольнике 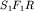 ; за время
; за время 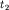 область возмущений будет заключена в треугольнике
область возмущений будет заключена в треугольнике  и так далее. Фронт некоторой новой волны, называемой головной, отделяющей область пространства, возмущенную упругими колебаниями, от невозмущенной, в момент
и так далее. Фронт некоторой новой волны, называемой головной, отделяющей область пространства, возмущенную упругими колебаниями, от невозмущенной, в момент 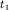 будет проходить вдоль прямой линии
будет проходить вдоль прямой линии  , в момент
, в момент 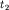 - вдоль линии
- вдоль линии  и так далее. Одной стороной фронт головной волны касается фронта отраженной из критической точки волны, другой примыкает к фронту скользящей преломленной волны. В точке
и так далее. Одной стороной фронт головной волны касается фронта отраженной из критической точки волны, другой примыкает к фронту скользящей преломленной волны. В точке 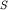 , где возникает головная волна, фронты отраженной и головной волн выйдут на поверхность одновременно, а далее отраженная волна, поскольку она имеет меньшую скорость, начнет отставать от головной.
, где возникает головная волна, фронты отраженной и головной волн выйдут на поверхность одновременно, а далее отраженная волна, поскольку она имеет меньшую скорость, начнет отставать от головной.
Из рис. 4.6 видно, что фронты головной преломленной волны будут плоскостями, наклоненными под углом  к границе раздела, а лучи, перпендикулярные фронту, будут наклонены под постоянным углом е к поверхности наблюдений. Фронт головной волны будет скользить вдоль линии наблюдений с кажущейся скоростью
к границе раздела, а лучи, перпендикулярные фронту, будут наклонены под постоянным углом е к поверхности наблюдений. Фронт головной волны будет скользить вдоль линии наблюдений с кажущейся скоростью  . Из треугольника
. Из треугольника  легко получить выражение для кажущейся скорости (закон кажущихся скоростей, закон Бенндорфа). В самом деле,
легко получить выражение для кажущейся скорости (закон кажущихся скоростей, закон Бенндорфа). В самом деле,  , отсюда
, отсюда  , т.е. для данной среды
, т.е. для данной среды  .
.
Установим связь между углом выхода сейсмической радиации  и углами
и углами  и
и  . Угол
. Угол  на рис. 4.7 равен углу
на рис. 4.7 равен углу  , а последний равен
, а последний равен  (как углы со взаимноперпендикулярными сторонами). Поэтому
(как углы со взаимноперпендикулярными сторонами). Поэтому 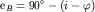 , отсюда
, отсюда  .
.
Индекс "B" взят для значений  и
и  по восстанию пласта. Если индексом "П" обозначить соответствующие значения по падению пласта, то нетрудно доказать, что
по восстанию пласта. Если индексом "П" обозначить соответствующие значения по падению пласта, то нетрудно доказать, что  . Точки
. Точки 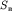 и
и  являются начальными точками преломленной волны. Между ними преломленные волны наблюдаться не могут, т.е. они выходят на земную поверхность на некотором расстоянии от пункта взрыва, сравнимом с глубиной залегания преломляющей границы.
являются начальными точками преломленной волны. Между ними преломленные волны наблюдаться не могут, т.е. они выходят на земную поверхность на некотором расстоянии от пункта взрыва, сравнимом с глубиной залегания преломляющей границы.
2. Вывод уравнения линейного годографа головной преломленной волны, образовавшейся над наклонной границей двух сред (прямая задача). Пусть под однородной покрывающей средой со скоростью распространения упругих волн 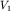 расположена плоская граница второго слоя с
расположена плоская граница второго слоя с  . Требуется получить уравнение годографа головной преломленной волны, т.е. установить теоретическую зависимость времени прихода волны (
. Требуется получить уравнение годографа головной преломленной волны, т.е. установить теоретическую зависимость времени прихода волны ( ) от расстояния (
) от расстояния ( ), скорости распространения упругих волн (
), скорости распространения упругих волн (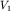 и
и 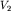 ), глубины залегания (
), глубины залегания ( ) и угла наклона (
) и угла наклона ( ) преломляющей границы (рис. 4.7).
) преломляющей границы (рис. 4.7).
Как показано выше, первой точкой профиля наблюдений, в которой начинает регистрироваться преломленная волна, является точка 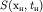 , называемая начальной точкой головной волны. Так как все лучи головной преломленной волны параллельны, то углы
, называемая начальной точкой головной волны. Так как все лучи головной преломленной волны параллельны, то углы  и
и  постоянны, а это значит, что линейный годограф преломленной волны имеет постоянный наклон к оси
постоянны, а это значит, что линейный годограф преломленной волны имеет постоянный наклон к оси  . Наклон к оси х остается постоянным лишь у прямой линии. Таким образом, годограф головной преломленной волны над плоской границей является прямой линией, начинающейся в точке
. Наклон к оси х остается постоянным лишь у прямой линии. Таким образом, годограф головной преломленной волны над плоской границей является прямой линией, начинающейся в точке 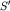 с координатами
с координатами  и
и  и наклоненной к оси
и наклоненной к оси  под углом
под углом  .
.

|
| Рис. 4.7. К выводу уравнения годографа головной преломленной волны |
Отсюда можно получить уравнение годографа преломленной волны. По восстанию пласта 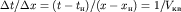 , где
, где  и
и  - координаты любой точки годографа. Очевидно, для получения уравнения необходимо определить
- координаты любой точки годографа. Очевидно, для получения уравнения необходимо определить  и
и  .
.
Возьмем мнимый пункт взрыва  и опустим перпендикуляры на О'A и ось
и опустим перпендикуляры на О'A и ось  . Из треугольника
. Из треугольника 
 , из треугольника OO'K OK = 2H sin i. Учитывая, что
, из треугольника OO'K OK = 2H sin i. Учитывая, что  , получим
, получим

|
Из треугольника О'AS и OO'A можно получить  и
и 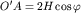 . Откуда
. Откуда 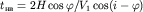 . Нетрудно показать, что для точек по падению границы
. Нетрудно показать, что для точек по падению границы

|
Учитывая, что  , получаем уравнение годографа преломленной волны:
, получаем уравнение годографа преломленной волны:

|
Проведя преобразования во втором слагаемом, можно получить окончательное уравнение годографа преломленной волны:
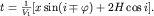
| (4.9) |
Причем знак "-" берется для годографа по восстанию границы (здесь волна приходит быстрее), знак "+" берется для годографа по падению границы от пункта взрыва. Из уравнений годографов видно, что при  , где
, где 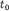 - время на пункте взрыва.
- время на пункте взрыва.
Для горизонтальной преломляющей границы ( )
)

| (4.10) |
Выражение для годографа преломленной волны можно записать в таком виде:

|
При  , что означает приход волны сначала к удаленным, а затем к близким к пункту взрыва точкам наблюдения. При
, что означает приход волны сначала к удаленным, а затем к близким к пункту взрыва точкам наблюдения. При  и
и  , что соответствует случаю, когда головная преломленная волна не сможет выйти на поверхность и работы методом МПВ невозможны. Поэтому этот метод может применяться для изучения не очень крутых структур, т.е. при углах падения, меньших 45
, что соответствует случаю, когда головная преломленная волна не сможет выйти на поверхность и работы методом МПВ невозможны. Поэтому этот метод может применяться для изучения не очень крутых структур, т.е. при углах падения, меньших 45  .
.
Преломленная волна на удалении 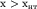 от пункта взрыва всегда приходит раньше отраженной и прямой волн и ее удобно регистрировать в области первых вступлений. Применяется также корреляционный метод преломленных волн (КМПВ), когда выделение преломленных волн производится и в последующих вступлениях.
от пункта взрыва всегда приходит раньше отраженной и прямой волн и ее удобно регистрировать в области первых вступлений. Применяется также корреляционный метод преломленных волн (КМПВ), когда выделение преломленных волн производится и в последующих вступлениях.
Как показано выше, годограф волны, преломленной на плоской границе двух сред, прямолинеен. Однако, если преломляющая граница криволинейна, то и годограф приобретает криволинейную форму. Это объясняется тем, что угол выхода сейсмической радиации  и кажущаяся скорость
и кажущаяся скорость  меняется при изменении угла наклона границы (
меняется при изменении угла наклона границы ( ) по профилю наблюдений, что приводит к изменению угла наклона годографа.
) по профилю наблюдений, что приводит к изменению угла наклона годографа.
Как отмечалось в 10.1.4, если в среде скорость упругих волн возрастает с глубиной, что может наблюдаться, например, при смене литологии или из-за увеличения давления, то возникают рефрагированные волны. Механизмы образования рефрагированных и скользящих преломленных волн имеют определенное сходство. С увеличением скорости с глубиной критический угол падения увеличивается и рефрагированные волны будут проходить во втором слое по дугообразным лучам (4.1, в). Выходя на поверхность земли, рефрагированные волны регистрируются подобно головным преломленным. Годографы преломленных и рефрагированных волн сходны между собой, и их распознавание имеет большое значение, так как позволяет избавиться от ошибок при интерпретации результатов сейсморазведки.
3. Обратная задача метода преломленных волн. Обратная задача метода преломленных волн (МПВ) над наклонной границей двух сред сводится к определению скоростей в верхнем (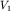 ) и нижнем (
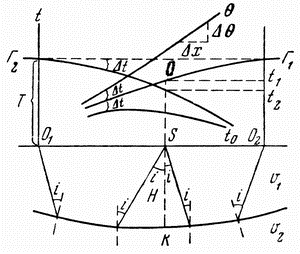
) и нижнем ( ) слоях и геометрических параметров разреза (Н, \varphi). Ее решают различными способами, основанными на анализе уравнения годографа (4.8) - (4.10). Как показывает практика интерпретации МПВ, наиболее надежно решить обратную задачу можно, имея встречные годографы (Г1 и Г2), которые получаются из двух точек взрыва О1 и О2, находящихся на концах изучаемого профиля (рис. 4.8).
) слоях и геометрических параметров разреза (Н, \varphi). Ее решают различными способами, основанными на анализе уравнения годографа (4.8) - (4.10). Как показывает практика интерпретации МПВ, наиболее надежно решить обратную задачу можно, имея встречные годографы (Г1 и Г2), которые получаются из двух точек взрыва О1 и О2, находящихся на концах изучаемого профиля (рис. 4.8).
|
Рис. 4.8. Определение граничной скорости с помощью разностного годографа и построение преломляющей границы способом 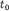
|
А. Определение граничной скорости по разностному годографу. Имея два встречных годографа, можно построить разностный годограф:  , где
, где  и
и 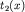 - время прихода головной преломленной волны в точку х по первому и второму (встречному) годографу,
- время прихода головной преломленной волны в точку х по первому и второму (встречному) годографу,  - время во взаимных точках, т.е. время прихода волны из О1 в О2 или из О2 в О1 (см. рис. 4.8). Легко видеть, что путь головной волны из пункта взрыва О1 в точку О2 и, наоборот, из пункта взрыва О2 в точку О1 одинаков, а значит, время во взаимных точках по встречным годографам одинаково и постоянно для данного интервала О1О2 (рис. 4.8).
- время во взаимных точках, т.е. время прихода волны из О1 в О2 или из О2 в О1 (см. рис. 4.8). Легко видеть, что путь головной волны из пункта взрыва О1 в точку О2 и, наоборот, из пункта взрыва О2 в точку О1 одинаков, а значит, время во взаимных точках по встречным годографам одинаково и постоянно для данного интервала О1О2 (рис. 4.8).
Взяв производную от уравнения разностного годографа, получим  , где
, где  - угловой коэффициент разностного годографа, равный обратной скорости, т.е.
- угловой коэффициент разностного годографа, равный обратной скорости, т.е.

|
Отсюда
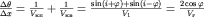
|
Таким образом, граничная скорость может быть определена по наклону разностного годографа  . При углах наклона, меньших 10 - 15
. При углах наклона, меньших 10 - 15  ,
, 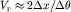 .
.
Б. Определение скорости в перекрывающем слое. Скорость упругих волн в перекрывающем слое (толще)  может быть оценена по точкам пересечения годографов прямой и головных преломленных волн:
может быть оценена по точкам пересечения годографов прямой и головных преломленных волн:  , где
, где  и
и 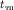 - координаты точек пересечения.
- координаты точек пересечения.
Однако более точно  получается по данным метода отраженных волн (10.3.2).
получается по данным метода отраженных волн (10.3.2).
В. Построение преломляющей границы способом нулевого времени. Одним из простых и точных способов определения 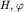 и построения преломляющей границы является способ нулевого времени (
и построения преломляющей границы является способ нулевого времени (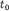 ).
).
Для любой точки 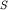 , где имеются два встречных годографа (см. рис. 4.8), можно найти некоторую функцию
, где имеются два встречных годографа (см. рис. 4.8), можно найти некоторую функцию  , которая равна времени на пункте взрыва
, которая равна времени на пункте взрыва  . В самом деле,
. В самом деле,  . Отсюда, считая границу на участке СD плоской и опустив из S перпендикуляр на СD, получим
. Отсюда, считая границу на участке СD плоской и опустив из S перпендикуляр на СD, получим
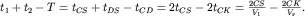
|
Из треугольника CSK: 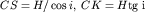 . Учитывая, что
. Учитывая, что  , получим:
, получим:
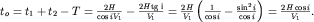
| (4.12) |
Следовательно, для любой точки профиля, где имеются встречные годографы, можно найти фиктивное время  , а затем и рассчитать
, а затем и рассчитать
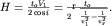
| (4.13) |
Практически применение способа 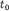 сводится к следующему. Для любой точки х определяется величина
сводится к следующему. Для любой точки х определяется величина  . От значения
. От значения 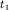 по первому годографу измерителем откладывается
по первому годографу измерителем откладывается 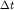 вверх (получаем точку разностного годографа
вверх (получаем точку разностного годографа 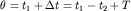 ) и вниз (получаем
) и вниз (получаем 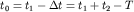 ). Сделав подобные построения в нескольких (3 - 5) точках оси х и соединив точки
). Сделав подобные построения в нескольких (3 - 5) точках оси х и соединив точки  и
и 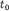 , получаем разностный годограф
, получаем разностный годограф 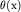 и линию
и линию 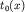 . По наклону разностного годографа находится граничная скорость
. По наклону разностного годографа находится граничная скорость 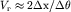 (при
(при  ). Если угол
). Если угол 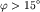 , то ее можно определить по формуле, приведенной выше (
, то ее можно определить по формуле, приведенной выше ( ). Зная
). Зная 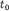 в каждой точке, по формуле (4.13) можно рассчитать эхо-глубину
в каждой точке, по формуле (4.13) можно рассчитать эхо-глубину  .
.
Проведя из нескольких точек х дуги радиусами  и соединив их плавной касательной, получим искомую преломляющую криволинейную границу раздела. Для криволинейной границы не имеет смысла говорить об угле наклона
и соединив их плавной касательной, получим искомую преломляющую криволинейную границу раздела. Для криволинейной границы не имеет смысла говорить об угле наклона  , поскольку он разный в разных точках преломляющей границы.
, поскольку он разный в разных точках преломляющей границы.
Приведенные прямые и обратные задачи МОВ и МПВ для двухслойного разреза являются основными задачами сейсморазведки, поскольку, заменив верхний слой ( ) толщей (
) толщей ( ), получаем практически одни и те же годографы. Решение кинематических прямых и обратных задач для отраженных, преломленных, рефрагированных, дифрагированных волн слоистых толщ (одномерные задачи - 1Д), сред с вытянутыми контактами (двухмерные задачи - 2Д) и для включений объектов (трехмерные задачи - 3Д) в аналитическом виде связано с большими математическими сложностями.
), получаем практически одни и те же годографы. Решение кинематических прямых и обратных задач для отраженных, преломленных, рефрагированных, дифрагированных волн слоистых толщ (одномерные задачи - 1Д), сред с вытянутыми контактами (двухмерные задачи - 2Д) и для включений объектов (трехмерные задачи - 3Д) в аналитическом виде связано с большими математическими сложностями.
Дата добавления: 2015-08-26; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Прямая и обратная задача отраженной волны для двухслойной среды с наклонной границей раздела. | | | Принципы решения обратной задачи метода рефрагированных волн. |