Принципы решения прямых задач сейсморазведки.

Прямой задачей сейсморазведки называется расчет времен прихода () и амплитуд () для той или иной волны для известного сейсмогеологического разреза, т.е. когда известны: мощности, глубины залегания, размеры тех или иных геологических объектов (чаще слоев) и скорости распределения упругих волн, а также место и форма источника. Строгое решение прямых динамических задач сейсмики неоднородных сред производится путем решения волнового уравнения вида:

(4.4)

где 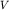- скорость той или иной волны ( 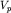или 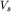), - амплитуда или иное возмущение сигнала, распространяющееся в среде () на разных временах после его возбуждения. Решение этого уравнения с использованием граничных условий очень сложно и его удается выполнить лишь для простых моделей сред. Значительно проще решать кинематические задачи, т.е. определять время прихода той или иной волны (прямой, отраженной, преломленной и др.) для известной модели, зная лишь положение источника и момент возбуждения упругой волны. Традиционно простейшим результатом решения прямой задачи является получение уравнения годографа, или аналитического выражения для с дальнейшим построением годографа - графика зависимости времени прихода той или иной волны () от расстояния от пункта возбуждения до пункта приема ().

Самой простой прямой задачей сейсморазведки является получение годографа прямой волны, т.е. задачи, которую в других геофизических методах называют задачей о нормальном поле (см. рис. 4.2). Очевидно, что время прихода прямой волны после создания упругого импульса в пункте возбуждения или взрыва (ПВ) равно 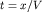. Поэтому линейный годограф имеет вид прямой линии. По наклону прямой линии можно определить скорость .

Рис. 4.2. К выводу уравнения прямой волны

Дата добавления: 2015-08-26