Прямая и обратная задачи над вертикально намагниченным шаром.

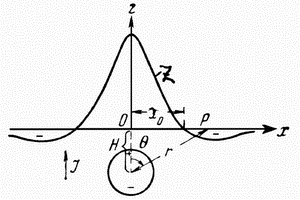
1. Прямая задача. Пусть вертикально намагниченный шар с центром на глубине залегает под началом координат (рис. 2.5). Необходимо определить напряженность поля вдоль профиля . Потенциал шара можно представить как потенциал диполя, помещенного в его центре. Поэтому, согласно (2.7), потенциал шара с магнитным моментом (или магнитной массой ), равен:

(2.10)

Рис. 2.5. Магнитное поле шара

Отсюда, взяв производные, найдем элементы магнитного поля шара:

(2.11)

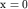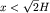
Анализ этих формул и построенных по ним графиков показывает, что над центром шара () будут а . При аномалии исчезают. При при , а при

Таким образом, в плане над шаром изолини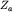и и 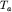будут иметь вид концентрических окружностей. При этом изолинии 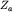будут двух знаков, а 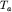- одного.

2. Обратная задача. Решение уравнений (2.11) теми же приемами, что и для столба, дает возможность по характерным точкам на графиках найти глубину центра вертикально намагниченного шара:

Ha=1,8 | xZ1/2 |=1,8| xZH |=1,5| xT1/2 |=0,7| xZ0 |=0,5| xZmin |=

(2.12)

где и - абсциссы точек половины - точки с точки с

Зная 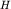, можно оценить магнитную массу шара ():

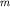Отсюда, так как то Если известны и 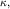можно определить объем шара.

Дата добавления: 2015-08-26