Прямая и обратная задачи над намагниченным вертикальным бесконечно длинным столбом (стержнем).

1. Прямая задача. Пусть на глубине 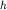залегает вершина бесконечно длинного столба (вертикального цилиндра или стержня) сечением (рис. 2.4). Его можно представить как тело одного полюса (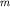) с интенсивностью намагничения (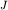), направленной вдоль оси z, и "магнитной массой" . Так как нижний полюс столба расположен очень далеко, то его влиянием можно пренебречь и считать, что вся "масса" сосредоточена на вершине столба.

Необходимо найти напряженность поля вдоль профиля x над телом. Потенциал от верхнего полюса столба в точке P будет равен потенциалу точечной массы (см.2.4):

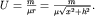
(2.7)

Составляющие поля выражаются производными потенциала по соответствующим осям координат:

(2.8)

Используя полученные формулы, можно построить графики напряженности поля (рис. 2.4). Легко видеть, что над столбом будут максимумы 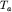и 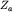, а значения их будут одного знака, положительные при вертикальной . Горизонтальная составляющая () слева будет иметь максимум, а справа - минимум. Вдалеке от столба аномалии исчезают. В плане над таким столбом изолини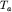и и 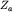будут иметь вид концентрических окружностей одного знака.

Рис. 2.4. Магнитное поле вертикального бесконечно длинного столба

2. Обратная задача. Решение уравнений (2.8) дает возможность по характерным точкам на графиках определить глубину залегания верхней кромки вертикального бесконечно длинного столба (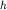). Так центр столба находится в точке, где а

Для точек, удаленных на расстояния от начала координат, в которых равно половине максимального

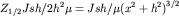
Решив это уравнение, получим h. Аналогичным образом находятся связи и между другими характерными точками , (экстремумы на составляющей ), 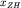(абсциссы точек пересечения и 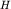). В результате получаются следующие формулы для расчета 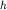по абсолютным значениям этих параметров:

(2.9)

Зная 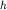, можно оценить величину магнитной массы:

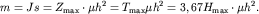
Так как , где 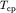- среднее значение полного вектора напряженности поля в изучаемом районе, а - магнитная восприимчивость столба, то

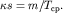
Отсюда, если известно \kappa по измерениям на образцах, можно определить площадь поперечного сечения столба ().

Дата добавления: 2015-08-26