
Читайте также:
|
Соображения, используемые при выборе проекций:
1) простота изображения и изучения по карте прикладных функций (плотность населения, курс судна, телекоммуникационные спутниковые линии связи);
2) возможность и точность измерений по карте (площадей, азимутов);
3) протяженность (N-Z или W-O) и целостность изображаемого объекта.
Так, например, по соображениям обеспечения точности при значительной протяженности с запада на восток для карты России наиболее часто применяют равнопромежуточную коническую проекцию Каврайского с сечениями по 47º и 62º северной широты (p £ 3%, w £ 2º).
По соображениям удобства прокладки курса судов используют равноугольную цилиндрическую проекцию, а для изображения телекоммуникаций и спутниковой связи - косую азимутальную стереографическую проекцию.
Карты мира обычно составляют в цилиндрических, псевдоцилиндрических и поликонических проекциях (рис. 3.13). Для уменьшения искажений часто используют секущие цилиндры, а псевдоцилиндрические проекции иногда дают с разрывами на океанах.
Карты полушарий всегда строят в азимутальных проекциях. Для западного и восточного полушарий естественно брать поперечные (экваториальные), для северного и южного полушарий — нормальные (полярные) (рис. 3.14), а в других случаях (например, для материкового и океанического) — косые азимутальные проекции.
Карты материков Европы, Азии, Северном и Южной Америки, Австралии с Океанией чаще всего строят в равновеликих косых азимутальных проекциях, для Африки берут поперечные, а для Антарктиды — нормальные азимутальные проекции.
Наиболее часто находят применение проекции: равноугольная поперечно-цилиндрическая проекция Гаусса-Крюгера (топографические карты) и видоизмененная простая поликоническая проекция (в международной карте мира М1:1000000).
Видоизмененная простая поликоническая проекция применяется как многогранная. Многогранные проекции получают путем, проектирования шара (эллипсоида) на поверхность касательного или секущего многогранника (рис. 1.15). Чаще всего каждая грань представляет собой равнобочную трапецию, хотя возможны и иные варианты (например, шестиугольник, квадрат, ромб). 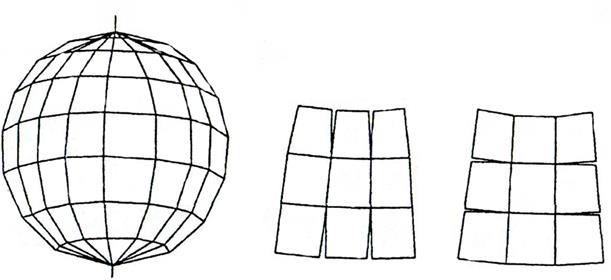
Рис. 1.15.Схема многогранной проекции и расположение листов карт
Многогранное представление является более ранним по происхождению, чем многополосное представление Гаусса-Крюгера. Земная поверхность, принимаемая за поверхность эллипсоида вращения, делится линиями меридианов и параллелей на трапеции (для М1:1000000 – 4º по широте и 6º по долготе). Трапеции изображаются на отдельных листах в одной и той же проекции.
Меридианы изображаются прямыми линиями. Длина двух меридианов, отстоящих от среднего на ±2ºпо долготе (на ±4º на сдвоенных листах и на ±8º на счетверенных), искажений не имеет. Крайние параллели каждого листа (северная и южная) являются дугами окружностей, центры этих параллелей находятся на среднем меридиане, длина их не искажается. Для построения внутренних параллелей используют способ Хинкса, то есть проводят эти параллели через точки, полученные путем деления всех меридианов на четыре равные части. Картографическая сетка строится через 1º по широте и по долготе (на сдвоенных листах – по долготе через 2º, на счетверенных – через 4º). Таким образом, все листы карты масштаба 1:1000000 имеют пять параллелей и семь меридианов. Так как криволинейные меридианы простой поликонической проекции заменяются в видоизмененной поликонической проекции прямыми, соединяющими соответствующие точки крайних параллелей, то масштабы на внутренних параллелях будут меньше единицы. Минимальный масштаб получается на средней параллели каждого листа карты. Для карты масштаба 1: 1000000 искажение длины средней параллели каждого листа – 0,06%.
На каждом листе имеются четыре точки, в которых отсутствуют искажения всех видов; эти точки находятся на пересечении крайних параллелей листа с меридианами, удаленными от среднего на 2º к западу и востоку. Максимальное искажение площади p находится в середине листа, оно имеет знак минус и может достигать -0,14%.Изоколы нулевых искажений площади имеют вид кривых, проходящих через точки, в которых отсутствуют искажения, и вытянутых вдоль крайних меридианов.
Достоинством видоизмененной простой поликонической проекции, применяемой как многогранная, является небольшая величина искажений. В пределах листа карты искажения длин не превышают 0,10%, площади - 0,15%, углов - 5' и являются практически неощутимыми. Недостаток этой проекции - появление разрывов при соединении листов по меридианам и параллелям.
Видоизмененная простая поликоническая проекция является одним из возможных типов проекций внутри многогранного представления. Из табл.1.1 видно, что при картографировании ограниченного пространства практически можно не учитывать искажений длин и считать в этом смысле различные равноугольные проекции практически равноценными. Что и оказалось важным при выборе многогранного представления.
Самой распространенной является равноугольная поперечная цилиндрическая проекция (Гаусса-Крюгера). Поверхность эллипсоида разделяется в этой проекции на сфероидические двуугольники (геодезические зоны). Такое представление создает разрывы по краям, но масштаб внутри каждой отдельной зоны практически постоянный.
Таблица 1.1
Дата добавления: 2015-08-26; просмотров: 154 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Соотношения между искажениями и распределение искажений на карте | | | Искажение длин в равноугольных проекциях |