Понятие о картографических проекциях. Классификация проекций по характеру искажений

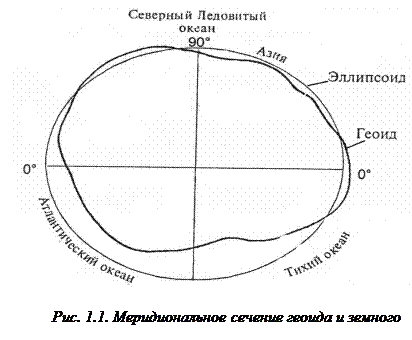
Известно, что Земля шарообразна, т.е. не обладает формой идеального шара. Фигура ее неправильна, и, как всякое вращаю­щееся тело, она немного сплюснута у полюсов. Сложную фигуру нашей планеты, ограниченную уровненной поверхностью океана, называют геоидом. Наилучшее геометрическое приближение к реальной фигуре Земли дает эллипсоид вращения — геометрическое тело, которое образуется при вращении эллипса вокруг его малой оси (рис. 1.1). Сжатие эллипсоида моделирует сжатие планеты у полюсов. На ри­сунке видно, насколько не совпадают меридиональные сечения геоида и земного эллипсоида.

При переходе от физической поверхности Земли к ее отображению на плоскости (на карте) выполняют две операции: 1)проектирование земной поверхности с ее сложным рельефом на поверхность земного эллипсоида, размеры которого установлены посредством геодезических и астрономических измерений, и 2)изображение поверхности эллипсоида на плоскости посредством одной из картографических проекций.

Вычисление и уточнение размеров земного эллипсоида, начатое еще в XVIII в., продолжается по сей день. Теперь для этого используют спутниковые наблюдения и точные гравиметрические измерения. Это непростая задача: нужно рассчитать геометрически правильную фигуру — референц-эллипсоид, который наилучшим образом приближен к геоиду и относительно которого выполняют все геодезические вычисления и рассчитывают картографические проекции.

В России принят референц-эллипсоид Ф.Н. Красовского вычисленный в 1940 г.

Его параметры таковы:

¾ большая полуось (а) - 6 378 245 м

¾ малая полуось (b) - 6 356 863 м

¾ сжатие (а-b)/а - 1:298,3

Картографическая проекция - математически определенный способ отображения поверхности земного эллипсоида на плоскость - задается парой уравнений: { x=f₁(B,L); y=f₂(B,L) }, где B - широта (latitude), L - долгота (longitude) отображаемой точки.

Поверхность эллипсоида (или шара) нельзя развернуть на плоскости подобно поверхности конуса или цилиндра. Поэтому непрерывность и однозначность отображения достигаются за счет неравномерного растяжения (или сжатия) поверхности земного эллипсоида при совмещении ее с плоскостью. Бесконечно малые окружности, взятые в разных точках на поверхности земного эллипсоида, в общем случае отображаются на плоскость в эллипсы, называемые эллипсами искажений (рис.1.2).

Это означает, что масштаб изображения зависит не только от положения точки, но может изменяться в данной точке с переменой направления. Различают главный масштаб (M), масштаб уменьшения Земли для изображения на плоскости, и частные масштабы: μ=dσ/ds, где ds - величина радиуса малой окружности на земном эллипсоиде в главном масштабе; dσ - величина этого отрезка, отложенного в заданном направлении на плоскости. На рис.1.1 показаны также: a,b - частные масштабы для главных направлений; m,n - частные масштабы для меридианов и параллелей, если они не совпадают с главными направлениями. Наряду с искажением длин, различают:

- искажение площадей p=dP'/dP, где dP' - площадь эллипса искажений, dP - площадь соответствующего малого круга на эллипсоиде;

- искажение углов ω - максимальное искажение угла между двумя линиями на эллипсоиде при изо­б­ра­жении его на карте.

В зависимости от искажений проекции кла­с­сифицируются сле­дующим образом.

Равноугольные проекции (conformal projection) сохраняют без искажений углы (ω =0) и формы малых объектов, но в них резко деформируются длины и площади объектов. В математике такие преобразования называют конформными. В каждой точке равноугольной проекции масштаб одинаков на всех направлениях, но меняется от точки к точке (рис.1.3,а). Эллипс искажений превращается в круг с диаметром, увеличивающимся к полюсу.

Равновеликие (рис.1.3,б) проекции (equivalente projection) не искажают площадей (p= 1), но в них искажены углы и формы объектов (вытянутость эллипсов искажений различна). Первый вид проекций приемлем для прокладки маршрутов транспортных средств, второй – для определения площадей и землепользования.

Рис.1.3,б. Эллипс искажений в равновеликой цилиндрической проекции

Произвольные проекции (arbitrary projection), которые не являются ни равноугольными, ни равновеликими, имеют искажения углов, площадей и длин, но эти искажения распределены по карте, например, так, что минимальные искажения имеются в центральной части и возрастают к краям. Среди произвольных проекций выделяют равнопромежуточные (equidistant projection) (рис.1.3,в), во всех точках которых масштаб по одному из главных направлений постоянен и равен главному масштабу (например, по меридианам или параллелям в проекциях, где они совпадают с главными направлениями). По своим свойствам равнопромежуточные проекции лежат между равноуголь­ными и равновеликими. Проекций вообще не имеющих искажений не существует.

Дата добавления: 2015-08-26