Читайте также:
|
6.1. Исходя из выражения (6.1), получить уравнения (6.2).
Решение:
Запишем уравнение 6.1: 
. Где 
Преобразуем уравнение 6.1.с учетом 
. Получаем систему уравнений:
6.2. Воспользовавшись уравнениями (6.1) и положив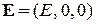 
и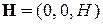 
, найти компоненты дрейфовой скорости электрона в 2DEG и компоненты тензора проводимости 
. Рассмотреть случай сильных магнитных полей (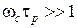
).
6.3. С учетом того, что компонента импульса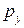 
является интегралом движения, свести гамильтониан (6.8) к гамильтониану линейного гармонического осциллятора.
Решение:
Запишем гамильтониан: 
координата центра волновой функции, 
- циклотронная частота. Следовательно 
6.4. Исходя из выражения (6.1) в отсутствии рассеяния, получить выражение (6.15) для групповой скорости частицы.
6.5. Показать, что период осцилляций 
есть 
.
Дата добавления: 2015-08-17; просмотров: 33 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи к гл. 5 | | | Реки и климат |