Задачи к гл. 5

5.1. Используя классическую механику, определить подвижность 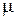и электропроводность 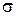идеального газа электронов. Считать, что время свободного пробега равно 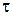, плотность электронного газа равна .

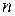Решение:

За время τ электрон набирает скорость 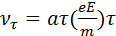и энергию 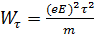. Пусть 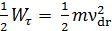. Следовательно 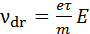. Тогда .

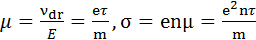5.3. Получить формулу (5.14).

Решение:

Рассмотрим левую часть равенства 5.14: 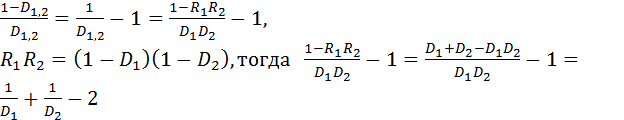Теперь рассмотрим левую часть равенства 5.14: 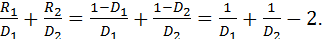Следовательно 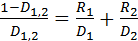ч.т.д.

5.4. Показать, что эффективная длина свободного пробега классической частицы определяется выражением .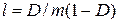

Решение:

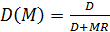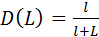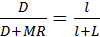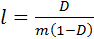Из выражения 5.15 следует, что , подставляя в это выражение значение M=mL и R=1-D, получаем выражение . Следовательно . Подставив в данное равенство значения M=mL и R=1-D, получим: . Следовательно ч.т.д.

5.5. Показать тождественность выражений (5.19) и (5.20).

Решение:

Из формулы 5.19 получается, что 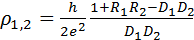, с учетом того, что R=1-D получаем:

Из выражения 5.20 следует, что 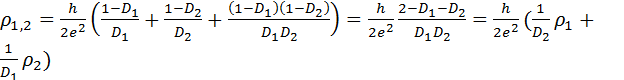ч.т.д.

5.6. Получить формулу (5.22).

Решение:

Рассмотрим формулу 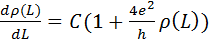до множим левую и правую части на 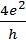и произведем замену переменных: 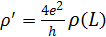. Тогда:

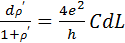. Проинтегрировав полувшееся диф. уравнение. Тогда 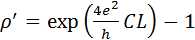. Следовательно .

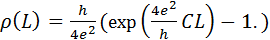5.7. Руководствуясь формулой (5.23), найти поправку второго порядка к .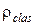

5.8. Получить выражение (5.37) для .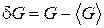

5.9. Доказать соотношение 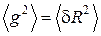. Сергей Юрьевич, возможно здесь пропущено δ в 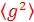? Задача решена именно для равенства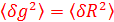

Решение:

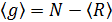, тогда . Тогда 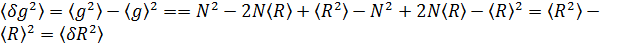ч.т.д.

5.10. Найти среднее значение произведения двух флуктуирующих величин 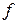и 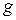, т.е. величину .

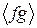5.11. Получить выражение (5.40).

5.12. Рассмотрим любую физическую систему, состоящую из 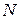статистически независимых одинаковых частей. Пусть 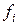− произвольная аддитивная величина, характеризующая -ю подсистему. Тогда в силу предполагаемой аддитивности соответствующая величина для всей системы будет 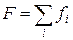. Найти величину .

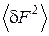Дата добавления: 2015-08-17