Читайте также:
|
Уравнение количества движения является также аналитическим выражением закона сохранения энергии. Применительно к газу уравнение количества движения записывается в виде обобщенного уравнения Бернулли:
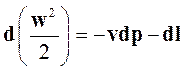, (2.19)
где W - скорость потока относительно стенок канала;
v,p - статические удельный объем и давление;
L– работа внешних сил и совершаемая потоком работа (считается положительной, если механическая энергия отводится от рабочей среды, и отрицательной, если механическая энергия сообщается среде).
В случае вращающегося канала
, (2.20)
где dlцс = udu - элементарная работа центробежной силы; dlтp - элементарная работа сил трения.
Интегрируя уравнение (2.20) в пределах от входного до выходного сечения канала, получим
При изоэнтропийном течении 1тр = 0, w2 = w2t, поэтому
(2.21)
Выражение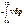 
можно проинтегрировать, если известна связь между v и р.
Для изоэнтропийного процесса 
, откуда 
, тогда
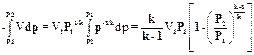. (2.22)
На основании уравнений (2.21) и (2.22) получим
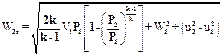. (2.23)
В осевых турбинах u1 = u2, поэтому
. (2.24)
Формула (2.24) справедлива и для неподвижного канала, придерживаясь ранее принятых обозначений (рис.2.1) и принимая u2=u1=0, имеем
(2.25)
Будучи записанными в полных параметрах выражения (2.25) и (2.24)
примут вид:
(2.26)
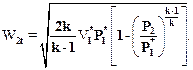(2.27)
Формулы (2.24) - (2.27) применяют при расчете газовых турбин. Для пара скорость потока на выходе из каналов следует определять по выражениям:
, (2.28)
(2.29)
Дата добавления: 2015-08-20; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Полные параметры рабочего тела. | | | Расход рабочей среды при изоэнтропийном течении. |