Поток рабочего тела в турбине. Уравнение неразрывности.

Поток рабочего тела в турбине

Поток рабочего тела взаимодействует с лопатками турбины. Энергетические преобразования в лопаточном аппарате сопровождаются изменением параметров рабочего тела, потерями энергии и утечками рабочего тела.

Состояние рабочей среды в рассматриваемой точке потока в конкретный момент времени характеризуется термодинамическими параметрами: давлением Р, температурой Т, удельным объемом v и плотностью ρ, кроме того, скоростью в абсолютном движении c или в относительном w. Скорость потока характеризуется безразмерными значениями скорости: числом Маха М, приведенной скоростью λ и т.д. Первое из них есть отношение скорости (c или w) к местной скорости звука в данной точки газового потока:

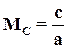или ,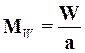

где: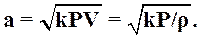

Для идеального газа, подчиняющегося уравнению Клапейрона-Менделеева pv = RT, формула (2.2) принимает частную форму:

.

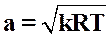Местная скорость звука a и число М меняются вдоль потока и различны в разных турбинах. В ускоряющемся потоке, например в соплах, скорость газа растет, температура и местная скорость звука уменьшаются, поэтому число М вдоль потока быстро увеличивается. В диффузорах - число М быстро падает. В турбинах возможны дозвуковые, околозвуковые и сверхзвуковые течения.

Приведенная скорость рабочего тела определяется как отношение скорости С к критической

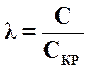
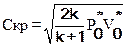
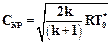
Приведенная скорость изменяется в том же направлении, что и число М, но слабее, чем число М, ввиду стабильности Скр.

Все реальные потоки рабочего тела в турбинах, строго говоря,-пространственные трехмерные течения вязкого сжимаемого газа. В теории турбомашин пользуются упрощенными моделями, достаточно точными для решения определенного круга конкретных задач и обладающими преимуществами наглядности результатов (например, двухмерные модели - плоское, цилиндрическое и коническое течения).

На практике во многих случаях параметры газа изменяются в основном вдоль, оси потока и зависят от одной координаты. Такого рода задачи наглядно и достаточно точно решаются при помощи одномерной модели течения. Во многих случаях заведомо двухмерные или трехмерные течения бывает полезно рассмотреть в рамках одномерной модели, так как это позволяет выявить физическую сущность основных процессов и закономерностей и отвлечься от второстепенных факторов. Одномерные течения могут быть прямоосными и кривоосными. Одномерная модель течения порождает представления о струйном течении, состоящем из системы прямых и кривых струек, в которых картина течения повторяется.

Уравнение неразрывности

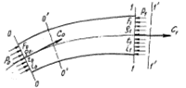
На основании закона сохранения массы расход газа во всех сечениях отдельной струйки газа неизменен. Поэтому для произвольно взятых контрольных сечений, проведенных перпендикулярно оси струйки, площадью F₀, F₁, F₂ (рис.2.1) можно написать:

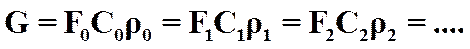, (2.6)

где С и ρ - соответственно скорость и плотность в рассматриваемых сечениях площадью F.

Рис.2.1 Параметры газа в контрольных сечениях струйки.

Дифференцируя уравнение расхода для произвольного сечения G= Fcρ, получаем Fcdρ + cρdF + Fρdc = 0. Разделив второе уравнение на первое, получил уравнение неразрывности в дифференциальной форме:

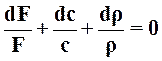
Дата добавления: 2015-08-20