
Читайте также:
|
Общие аналитические показатели
| xi | fi | xi fi | 
| 
| 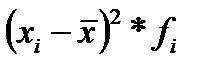
| 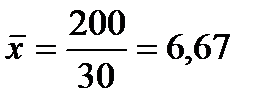

| ||||||
| -6,67 | 30,25 | 133,33 | ||||||||||
| -5,67 | 44,44 | 128,44 | ||||||||||
| -4,67 | 32,11 | 65,33 | ||||||||||
| -3,67 | 21,78 | 26,89 | ||||||||||
| -2.67 | 13,44 | 28,44 | ||||||||||
| -1,67 | 7,11 | 2,78 | ||||||||||
| -0,67 | 2,78 | 0,44 | ||||||||||
| 1,33 | 0,44 | 5,33 | ||||||||||
| 2,33 | 1,78 | 5,44 | ||||||||||
| 3,33 | 5,44 | 22,22 | ||||||||||
| 4,33 | 11,11 | 18,78 | ||||||||||
| 5,33 | 18,78 | 28,44 | ||||||||||
| 7,33 | 28,44 | 53,78 | ||||||||||
| 8,33 | 53,78 | 69,44 | ||||||||||
| 16,33 | 69,44 | 266,78 | ||||||||||
| 22,33 | 266,78 | 498,78 | ||||||||||
| Σ | * | 498,78 | 1354,67 | |||||||||
Внутригрупповая дисперсия обучающихся на младших курсах
| xi | fi | xi fi | 
| 
| 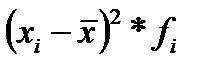
| 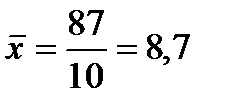

|
| -7,7 | 59,29 | 52,29 | ||||
| -6,7 | 44,89 | 89,78 | ||||
| -4,7 | 22,09 | 22,09 | ||||
| -0,7 | 0,49 | 0,98 | ||||
| 1,3 | 1,69 | 1,69 | ||||
| 2,3 | 5,29 | 5,29 | ||||
| 3,3 | 10,89 | 10,89 | ||||
| 20,3 | 412,09 | 412,09 | ||||
| Σ | * | * | 602,1 |
Внутригрупповая дисперсия обучающихся на средних курсах
| xi | fi | xi fi | 
| 
| 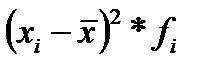
| 

|
| -5,2 | 27,04 | 54,08 | ||||
| -4,2 | 17,64 | 35,28 | ||||
| -3,2 | 10,24 | 10,24 | ||||
| -2,2 | 4,84 | 4,84 | ||||
| -1,2 | 1,44 | 1,44 | ||||
| 2,8 | 7,84 | 7,84 | ||||
| 4,8 | 23,04 | 23,04 | ||||
| 17,8 | 316,84 | 316,84 | ||||
| Σ | * | * | 453,60 |
Внутригрупповая дисперсия обучающихся на старших курсах
| xi | fi | xi fi | 
| 
| 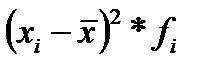
| 

|
| -6,1 | 37,21 | 37,21 | ||||
| -5,1 | 26,01 | 26,01 | ||||
| -3,1 | 9,61 | 9,61 | ||||
| -2,1 | 4,41 | 8,82 | ||||
| -1,1 | 1,21 | 1,21 | ||||
| 0,1 | 0,01 | 0,01 | ||||
| 2,9 | 8,41 | 8,41 | ||||
| 7,9 | 62,41 | 62,41 | ||||
| 8,9 | 79,21 | 79,21 | ||||
| Σ | * | * | 232,9 |
Средняя из внутригрупповых дисперсий: 
Межгрупповая дисперсия: 



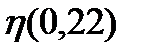 ; Коэффициент Этта больше коэф. Гамма, это свидетельствует о криволинейности связи.
; Коэффициент Этта больше коэф. Гамма, это свидетельствует о криволинейности связи.
Определение значимости n- коэффициента с помощью Z-критерия
Z=  Zкр = 2,32, при a = 0, 01. Различия значимы.
Zкр = 2,32, при a = 0, 01. Различия значимы.
Вывод:
Связь криволинейная. Таким образом, с вероятностью ошибки 0,01 мы можем утверждать, что значимость достижения высокого статуса зависит от курса обучения, подтверждается альтернативная гипотеза. Полученные данные можно распространять на генеральную совокупность.
Таблица 6 – Значимость сфер жизни, чел.
| Ранги | Образование | Семья | Отдых | Благосостояние | Карьера | Хобби | Работа |
| Итого |
Решение:
Образование
| Xk | Fk | Xk fk | 
| 
| I= 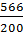 =2,83 =2,83
|
| 3,35 | 247,9 | ||||
| -0,69 | 28,29 | ||||
| 0,03 | 0,57 | ||||
| 1,37 | 24,66 | ||||
| 4,71 | 61,23 | ||||
| 10,05 | 291,45 | ||||
| 17,39 | 104,34 | ||||
| Σ | 37,59 | 758,44 |
Семья
| Xk | Fk | Xk fk | 
| 
| I= 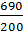 =3,45 =3,45
|
| 6,00 | 258,00 | ||||
| 2,10 | 77,70 | ||||
| 0,20 | 4,40 | ||||
| 0,30 | 12,90 | ||||
| 2,40 | 52,80 | ||||
| 6,50 | 39,00 | ||||
| 12,60 | 340,20 | ||||
| Σ | 30,1 | 758,00 |
Отдых
| Xk | Fk | Xk fk | 
| 
| I=  =4,63 =4,63
|
| 13,18 | 355,86 | ||||
| 6,92 | 83,04 | ||||
| 2,66 | 47,88 | ||||
| 0,40 | 3,60 | ||||
| 0,14 | 8,12 | ||||
| 1,88 | 71,44 | ||||
| 5,62 | 213,56 | ||||
| Σ | 30,8 | 783,50 |
Благосостояние
| Xk | Fk | Xk fk | 
| 
| I=  =4,27 =4,27
|
| 10,70 | 64,20 | ||||
| 5,15 | 175,10 | ||||
| 1,61 | 45,08 | ||||
| 0,07 | 2,80 | ||||
| 0,53 | 15,37 | ||||
| 2,99 | 149,50 | ||||
| 7,45 | 96,85 | ||||
| Σ | 28,5 | 548,90 |
Карьера
| Xk | Fk | Xk fk | 
| 
| I=  =3,9 =3,9
|
| 8,41 | 168,20 | ||||
| 3,61 | 126,35 | ||||
| 0,81 | 28,35 | ||||
| 0,01 | 0,34 | ||||
| 1,21 | 37,51 | ||||
| 4,41 | 92,61 | ||||
| 9,61 | 230,64 | ||||
| Σ | 28,07 | 684,00 |
Хобби
| Xk | Fk | Xk fk | 
| 
| I=  =5,18 =5,18
|
| 14,47 | 192,17 | ||||
| 10,11 | 121,32 | ||||
| 4,75 | 90,25 | ||||
| 1,39 | 33,36 | ||||
| 0,03 | 0,84 | ||||
| 0,67 | 22,11 | ||||
| 3,31 | 241,63 | ||||
| Σ | 37,73 | 701,68 |
Работа
| Xk | Fk | Xk fk | 
| 
| I=  =3,85 =3,85
|
| 8,12 | 154,28 | ||||
| 3,42 | 88,28 | ||||
| 0,72 | 41,76 | ||||
| 0,02 | 0,60 | ||||
| 1,32 | 31,68 | ||||
| 4,62 | 78,54 | ||||
| 9,92 | 257,92 | ||||
| Σ | 28,14 | 653,7 |
Итог:
| Сфера жизни | Индекс | Дисперсия доли | Ошибка выборки |
| Образование | 2,83 | 3,79 | 0,27 |
| Семья | 3,45 | 3,93 | 0,27 |
| Работа | 3,85 | 3,27 | 0,25 |
| Карьера | 3,90 | 3,42 | 0,26 |
| Благосостояние | 4,27 | 2,75 | 0,23 |
| Отдых | 4,63 | 3,91 | 0,27 |
| Хобби | 5,19 | 3,51 | 0,26 |
Вывод:
С помощью условного индекса мы сравнили объекты по отношению к одной и той же совокупности людей. По таблице можно утверждать, что самая значимая сфера жизни это сфера образования, далее следуют семейные ценности. Здесь видны значимые различия, т.к. суммарная ошибка меньше разности долей. Эти тенденции можно перенести на генеральную совокупность. Работа, карьера, благосостояние и отдых имеют средние значения в ранжированном ряду. Хобби наименее значимая сфера жизни, эти данные тоже можно распространять на ген. совокупность т.к. суммарная ошибка меньше разности долей и отсюда следует, что различия значимы.
Таблица 7 – Проведение свободного времени в зависимости от формы обучения, в абсолютных цифрах
| Занятие | В целом по массиву | Форма обучения | |
| Бюджет | Контракт | ||
| Смотрю телевизор | |||
| Общаюсь с друзьями | |||
| Общаюсь с семьей | |||
| Играю в компьютерные игры | |||
| Общаюсь через интернет | |||
| Читаю газеты, книги, журналы | |||
| Хожу на дискотеки | |||
| Количество опрошенных |
H1- проведение свободного времени зависит от формы обучения;
H0 - проведение свободного времени не зависит от формы обучения.
Зависимая переменная – проведение свободного времени, поливариантная, номинальная;
Независимая переменная – форма обучения, альтернативная, номинальная.
Решение:
| Занятие | Форма обучения | В целом по массиву | |||
| Бюджет | % | Контракт | % | ||
| Общаюсь с друзьями | 63,5 | 62,00 | |||
| Общаюсь через интернет | 34,0 | 49,00 | |||
| Общаюсь с семьей | 38,0 | 18,10 | |||
| Хожу на дискотеки | 36,0 | 22,00 | |||
| См. телевизор | 34,5 | 23,6 | |||
| Играю в компьютерные игры | 18,0 | 36,40 | |||
| Читаю газеты, журналы | 10,0 | 36,40 | |||
| Количество опрошенных | - | - |

| 
| 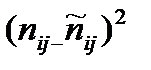
| 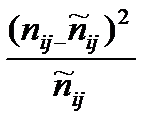
| χ2эмп = 31,327 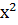 кр = 16,812
df = (7–1) (2–1) = 6, при a= 0,01 Различия значимы. кр = 16,812
df = (7–1) (2–1) = 6, при a= 0,01 Различия значимы.
 = = 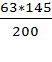 =45,675 =45,675
| |
| 45,675 | 18,7 | 0,410 | |||
| 91,350 | 0,4 | 0,004 | |||
| 47,125 | 62,0 | 1,316 | |||
| 33,350 | 54,0 | 1,619 | |||
| 60,900 | 15,2 | 0,250 | |||
| 25,375 | 107,6 | 4,603 | |||
| 46,400 | 31,4 | 0,677 | |||
| 17,325 | 18,7 | 1,079 | |||
| 34,650 | 0,4 | 0,012 | |||
| 17,875 | 62,0 | 3,469 | |||
| 12,650 | 54,0 | 4,269 | |||
| 23,100 | 15,2 | 0,658 | |||
| 9,625 | 107,6 | 11,179 | |||
| 17,600 | 31,36 | 1,782 | |||
| Σ | 578,56 | 31,327 | |||
Оценка силы и направления связи, к. Крамера:

Таким образом, мы видим, что связь средняя. Направление связи оценить невозможно, так как оба признака замерены на номинальном уровне.
Вывод по гипотезе и интерпретация результатов:
С вероятностью ошибки менее 0,01 можем утверждать, что форма обучения влияет на способы проведения досуга, т.е. данные позволяют нам принять альтернативную гипотезу.
Таблица 8 – Табличный вопрос «Степень допустимости нарушений моральных норм» (частота)
| Подвопросы: | Недопустим ни при каких обстоятельствах | Можно себе позволить в зависимости от ситуации | Не считаю это предосудительным | Итого |
| Измена родине | ||||
| Обогащение за счет других | ||||
| Ложь и лицемерие | ||||
| Уклонение от службы в армии | ||||
| Супружеская измена | ||||
| Аморальное поведение в общественных местах | ||||
| Употребление наркотических веществ | ||||
| Получение/дача взяток | ||||
| Проституция | ||||
| Безбилетный проезд в общественном транспорте | ||||
| Проявление неуважения к старшему поколению | ||||
| Кража чужого имущества | ||||
| Использование ненормативной лексики в общественных местах |
Решение:
Измена родине I =  = 0,13
= 0,13
| xi | fi | xi fi | 
| 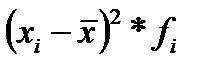
|
| 0,02 | 32,65 | |||
| 0,5 | 0,14 | 4,65 | ||
| 0,76 | 6,81 | |||
| Σ | - | 14,12 |
Обогащение за счет других I=  =0,25
=0,25
| xi | fi | xi fi | 
| 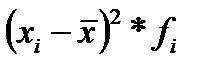
|
| 0,06 | 6,95 | |||
| 0,5 | 40,5 | 0,06 | 4,96 | |
| 0,56 | 5,59 | |||
| Σ | 50,5 | - | 17,50 |
Ложь и лицемерие I= 48,5/200= 0,24
| xi | fi | xi fi | 
| 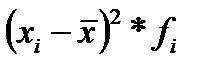
|
| 0,06 | 7,12 | |||
| 0,5 | 30,5 | 0,07 | 4,04 | |
| 0,57 | 10,33 | |||
| Σ | 48,5 | - | 21,49 |
Уклонение от службы в армии I= 91/200=0,46
| xi | fi | xi fi | 
| 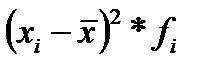
|
| 0,21 | 10,14 | |||
| 0,5 | 0,00 | 0,24 | ||
| 0,30 | 9,21 | |||
| Σ | - | 19,60 |
Супружеская измена I=22,5/200=0,11
| xi | fi | xi fi | 
| 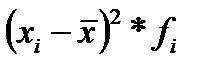
|
| 0,01 | 2,03 | |||
| 0,5 | 17,5 | 0,15 | 5,26 | |
| 0,79 | 3,94 | |||
| Σ | 22,5 | - | 11,22 |
Аморальное поведение в общественных местах I=34,5/200=0,17
| xi | fi | xi fi | 
| 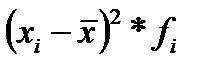
|
| 0,03 | 4,28 | |||
| 0,5 | 21,5 | 0,11 | 4,61 | |
| 0,68 | 8,90 | |||
| Σ | 34,5 | - | 17,80 |
Употребление наркотических веществ I=18,5/200=0,09
| xi | fi | xi fi | 
| 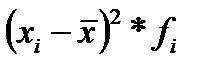
|
| 0,01 | 1,51 | |||
| 0,5 | 4,5 | 0,17 | 1,49 | |
| 0,82 | 11,53 | |||
| Σ | 18,5 | - | 14,54 |
Получение, дача взяток I=48/200=0,24
| xi | fi | xi fi | 
| 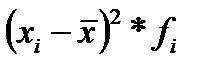
|
| 0,06 | 0,3 | |||
| 0,5 | 0,07 | 5,32 | ||
| 0,6 | ||||
| Σ | - | 11,62 |
Проституция I=28/200= 0,14
| xi | fi | xi fi | 
| 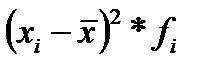
|
| 0,02 | 3,26 | |||
| 0,5 | 0,13 | 2,34 | ||
| 0,73 | 13,8 | |||
| Σ | - | 19,47 |
Безбилетный проезд в общественном транспорте I =100,5/200=0,5
| xi | fi | xi fi | 
| 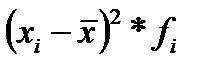
|
| 0,25 | 9,75 | |||
| 0,5 | 60,5 | |||
| 0,25 | ||||
| Σ | 100,5 | - | 19,75 |
Проявление неуважения к старшему поколению I=17,5/200=0,08
| xi | fi | xi fi | 
| 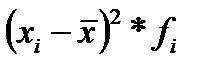
|
| 0,006 | 1,03 | |||
| 0,5 | 10,5 | 0,18 | 3,78 | |
| 0,84 | 5,88 | |||
| Σ | 17,5 | - | 10,69 |
Кража чужого имущества I=15,5/200=0,07
| xi | fi | xi fi | 
| 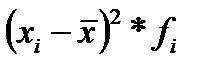
|
| 0,004 | 0,7 | |||
| 0,5 | 10,5 | 0,18 | 3,78 | |
| 0,9 | 4,5 | |||
| Σ | 15,5 | - | 8,98 |
Использование ненормативной лексики в общественных местах I=47,5/200=0,24
| xi | fi | xi fi | 
| 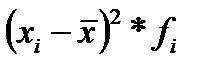
|
| 0,005 | 0,6 | |||
| 0,5 | 32,5 | 0,07 | 4,5 | |
| 0,6 | ||||
| Σ | 47,5 | - | 14,1 |
Итоговая таблица:
| Подвопросы: | Индексы | Дисперсия доли | Ошибка выборки |
| Измена родине | 0,13 | 0,07 | 0,037 |
| Обогащение за счет других | 0,25 | 0,09 | 0,041 |
| Ложь и лицемерие | 0,24 | 0,11 | 0,045 |
| Уклонение от службы в армии | 0,45 | 0,10 | 0,043 |
| Супружеская измена | 0,11 | 0,06 | 0,033 |
| Аморальное поведение в общественных местах | 0,17 | 0,09 | 0,041 |
| Употребление наркотических веществ | 0,09 | 0,07 | 0,037 |
| Получение/дача взяток | 0,24 | 0,09 | 0,041 |
| Проституция | 0,14 | 0,10 | 0,043 |
| Безбилетный проезд в общественном транспорте | 0,5 | 0,10 | 0,044 |
| Проявление неуважения к старшему поколению | 0,08 | 0,05 | 0,032 |
| Кража чужого имущества | 0,07 | 0,05 | 0,029 |
| Использование ненормативной лексики в общественных местах | 0,24 | 0,10 | 0,044 |
Вывод:
С помощью условного индекса мы сравнили объекты по отношению к одной и той же совокупности частот. По таблице можно утверждать, что по отношению ко всем объектам суммарная ошибка меньше разности долей, эти тенденции можно перенести на генеральную совокупность, следовательно, различия значимы.
Таблица 9 – Допустимость использования ненормативной лексики в общественных местах в зависимости от уровня дохода семьи, в абсолютных цифрах
| Допустимость | Уровень дохода семьи | |||||
| Высокий | Выше среднего | Средний | Ниже среднего | Низкий | Итого | |
| Недопустимо ни при каких обстоятельствах | ||||||
| Можно себе позволить в зависимости от ситуации | ||||||
| Не считаю это предосудительным | ||||||
| Итого: | 199* |
* Не ответил 1 из 200 объектов (0,5%).
H1 – допустимость использования ненормативной лексики в общественных местах зависит от уровня дохода;
H0 - допустимость использования ненормативной лексики в общественных местах не зависит от уровня дохода.
Зависимая переменная: использование ненормативной лексики, альтернативная, порядковая;
Независимая переменная: доход семьи, альтернативная, порядковая.
Определение величины 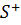
| Допустимость | Уровень дохода семьи | |||||
| Высокий | Выше среднего | Средний | Ниже среднего | Низкий | Итого | |
| Недопустимо ни при каких обстоятельствах | *1610 | - | ||||
| Можно себе позволить в зависимости от ситуации | - | |||||
| Не считаю это предосудительным | - | - | - | - | - | |
| Итого: |
*1610 = 23* (29+4+28+3+1+2+1+2)=1610
Определение величины 
| Допустимость | Уровень дохода семьи | |||||
| Высокий | Выше среднего | Средний | Ниже среднего | Низкий | Итого | |
| Недопустимо ни при каких обстоятельствах | - | *0 | ||||
| Можно себе позволить в зависимости от ситуации | - | |||||
| Не считаю это предосудительным | - | - | - | - | - | |
| Итого: |
*0=0*(1+2+28+3+29+4+6+4)=0

Для определения значимости коэффициента, рассчитаем t- критерий Стьюдента: 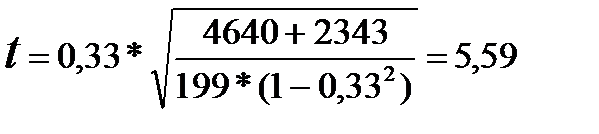 при α=0,01. Коэффициент значим.
при α=0,01. Коэффициент значим.
Статистический вывод:
С вероятностью ошибки менее 0,01 мы можем утверждать, что между переменными существует средняя прямая связь.
Таблица 10 – Сравнительная характеристика друзей и нормативного представления о «Герое нашего времени», чел.
| Объект | Значения | Доброта | Милосердие | Целеустремленность | Патриотизм | Инициативность | Честность | Общественная значимость | Терпимость |
| Друг | |||||||||
| -1 | |||||||||
| -2 | |||||||||
| -3 | – | – | – | ||||||
| Итого | |||||||||
| «Герой нашего времени» | |||||||||
| -1 | |||||||||
| -2 | – | – | – | – | |||||
| -3 | – | ||||||||
| Итого | |||||||||
| Озлобленность | Жестокость | Неопределенность | Отсутствие патриотизма | Пассивность | Подлость | Личный интерес | Нетерпимость |
xi fi


Интерпретация результатов:
При помощи средней арифметической взвешенной, мы сравниваем 2 группы совокупностей по одинаковому набору характеристик. Можно сказать, что по объекту «Друг» суммарная ошибка меньше дисперсии, т.е. есть тенденции, которые мы можем перенести с выборочной совокупности на генеральную. В группе «Герой нашего времени» аналогичная ситуация, дисперсия доли больше чем ошибка, а значит, в обеих группах различия значимы.
Дата добавления: 2015-08-17; просмотров: 33 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Показатели вариации | | | Преимущества неметаллической композитной арматуры. |