Раздел 5. Игровые задачи оптимизации решений

38. Постановка задачи «игра с природой». Стратегии игроков. Платежная матрица

39. Критерии при принятии решений в теории игр - принцип недостаточного обоснования Лапласа. Критерий обобщенного максимина (пессимизма — оптимизма) Гурвица.

40. Критерии при принятии решений в теории игр - максиминный критерий Вальда. Критерий обобщенного максимина (пессимизма — оптимизма) Гурвица.

41. Критерии при принятии решений в теории игр - минимаксный критерий Сэвиджа. Критерий Байеса.

Задачи

1. Найти экстремум функции

2. Найти экстремум функции

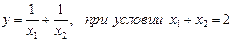
3. Привести ЗЛП к канонической форме

4. Написать двойственную ЗЛП

5. Написать двойственную ЗЛП

6. Написать двойственную ЗЛП

7.Найти графическим методом оптимальный план задачи линейного программирования.

8.Найти графическим методом оптимальный план задачи целочисленного линейного программирования.

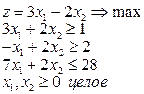9. Привести транспортную задачу к задаче закрытого типа и найти начальный план.

ai	bj

10. Построить множество Парето для двухкритериальной задачи

0 ≤ x ≤ 2

0 ≤ y ≤ 2

F= { f₁; f₂ }→opt. f₁= 5 x-y+ 2; f₂=-x+ 3 y+ 2

11. Написать детерминированный эквивалент задачи стохастического программирования распределения двух видов ресурсов для выпуска двух наименований изделий в M-постановке Ее модель:

где a_ij, b_i, c_j — случайные.

12. Определить оптимальную стратегию по четырем критериям:

1) принцип недостаточного обоснования Лапласа;

2) критерию обобщенного максимина (пессимизма — оптимизма) Гурвица;

3) максиминный критерий Вальда;

4) критерий обобщенного максимина (пессимизма — оптимизма) Гурвица,

для игры, заданной следующей платежной матрицей:

13. Составить математическую модель следующей задачи

14. Составить математическую модель следующей задачи

15. Составить математическую модель следующей задачи

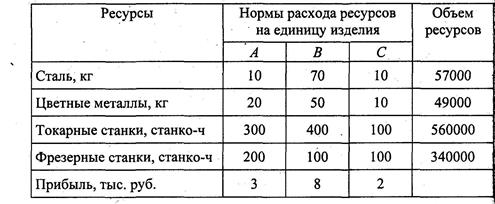
16. Составить математическую модель следующей задачи

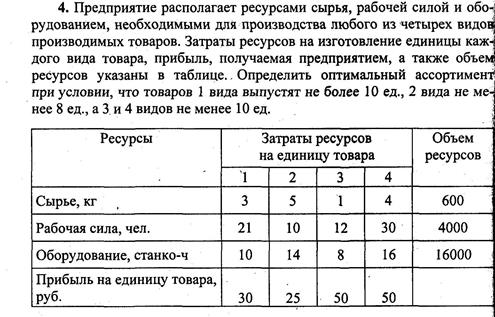
17. Составить математическую модель следующей задачи

18. Составить математическую модель следующей задачи

19. Составить математическую модель следующей задачи

20. Составить математическую модель следующей задачи

21. Составить математическую модель следующей задачи

Дата добавления: 2015-08-20