Основные Законы алгебры логики

Ø Операции с константами: a + 0 = a a + 1 = 1 a * 0 = 0 a * 1 = a

Ø Закон исключенного третьего: a + a = 1

Ø Закон непротиворечия: a * a = 0

Ø Законы идемпотенции: a + a = a a * a = a

Ø Закон двойного отрицания: a = a

Ø Законы де Моргана: a + b = a * b a * b = a + b

Ø Закон поглощения: a + a * b = a

Ø Закон склеивания: a * b + a * b = a

Сын: можно мне пойти в кино или купить мороженое?
Мама: нет

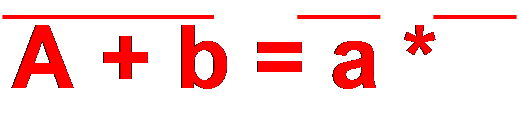
Нельзя пойти в кино и нельзя купить мороженое

Порядок выполнения операций можно изменять с помощью скобок:

Переместительный закон: a + b = b + a
Сочетательный закон: a+(b+с)=(a+b)+с
Дистрибутивныйзакон: a*(b+с)=(a*b)+(а*с)

18. Правила построения логических выражений в СДНФ.

Совершенная дизъюнктивная нормальная форма (СДНФ) — это булева функция, представленная в виде дизъюнкции элементарных конъюнкций, причём в каждой конъюнкции присутствуют все переменные, входящие в формулу, либо их отрицание.

Основные свойства СДНФ:

- в СДНФ нет двух одинаковых конъюнктивных термов;

- в СДНФ ни один конъюнктивный терм не содержит двух одинаковых множителей (переменных);

- в СДНФ ни один конъюнктивный терм не содержит вместе с переменной и ее отрицание.

На основании этих свойств получение СДНФ из таблицы истинности производится по правилу:

- из таблицы истинности выбираются все наборы значений аргументов x1,x2,…,xn, на которых функция равна 1;

- для каждого из таких наборов составляются конъюнкции из n переменных (причем, переменная входит в конъюнкцию с отрицанием, если ее значение на этом наборе равно 0, и без отрицания, если ее значение равно 1);

- полученные конъюнкции соединяются знаками дизъюнкции. (взято из интернета)

или как диктовал Маринкин: «Для всех строк с единичным значением выходной функции, выписывается логическая сумма(дизъюнкция) из логических произведений(конъюнкций) всех входных переменных, при этом входная переменная пишется с инверсией, если ее значение в соответствующей строке равно нулю».

19) История компьютера. Принципы организации работы компьютера. Базовая архитектура компьютера. Поколения ЭЦВМ.

Дата добавления: 2015-08-17