Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины.

Пусть задан закон распределения случайной величины x.

x	х 1	х 2	х 3	¼	хn
P	p 1	p 2	p 3	¼	pn

Математическое ожидание М x (или М (x)) случайной величины x определяется формулой

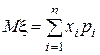
Дисперсия D xслучайной величины x определяется формулой

D x = M (x – M x)².

Дисперсия случайной величины — это математическое ожидание квадрата отклонения случайной величины от её математического ожидания.

1. Парная корреляция

2. Множественная регрессия

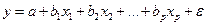Уравнение множественной регрессии

Цель множественной регрессии:

Построить модель с большим числом факторов, определив влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый фактор.

Спецификация модели включает в себя два круга вопросов:

- отбор факторов;

- выбор вида уравнения регрессии.

Отбор факторов:

· Требования к включаемым факторам:

количественно измеримы;

не должны находиться в точной функциональной связи или быть сильно коррелированы.

Этапы отбора факторов:

· исходя из сущности проблемы;

· на основе корреляционной матрицы и - статистики параметров регрессии

1) Проверка парной корреляции.

Принцип исключения факторов:

Если две переменные явно коллинеарны (), то одну из них исключаем.

Включаем фактор, имеющий наименьшую тесноту связи с другими факторами

2) Оценка мультиколлинеарности факторов (когда более, чем два фактора связаны между собой линейной зависимостью):

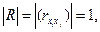Проверка гипотезы H0:

R – матрица коэффициентов корреляции.

Чем ближе к 1 определитель матрицы межфакторной корреляции, тем

меньше мультиколлинеарность факторов

Оценка параметров уравнения множественной регрессии

• Метод:

– а) метод наименьших квадратов (МНК)

– б) метод наименьших квадратов (МНК) для стандартизованного уравнения

• Схема: решение системы нормальных уравнений

Дата добавления: 2015-08-18