
Читайте также:
|
 ,
,
де l ОА – дійсна довжина кривошипа ОА, м;
ОА – довжина відрізка в мм, що зображує кривошип 1 на плані механізма.
Тепер креслярські розміри решти ланок відповідно дорівнюють:

В прийнятому масштабі викреслюється кінематична схема механізма для чотирьох рівновіддалених положень кривошипа ОА. За початкове положення кривошипа (0) приймається його положення вздовж горизонтальної осі вліво. Зображаємо траєкторію точки А кривошипа 1, яку ділимо на чотири рівні частини. Нумеруємо точки поділу А 0, А І, А ІІ, А ІІІ у напрямі обертання кривошипа. Положення точки В знаходимо методом засічок. Від точки А радіусом АВ робимо дугові засічки на траєкторії точки В. Нумеруємо відповідно точки перетину В 0, В І, В ІІ, В ІІІ. Сполучаємо відповідні точки А з точками В. Одержуємо плани положень ланок механізму. Для кожного положення на ланці 2 фіксуємо положення точки D: D 0, D І, D ІІ, D ІІІ.
4. Побудова планів швидкостей
Побудова планів швидкостей розглядається для II положення механізма (див. креслення-вкладку) і здійснюється в такій послідовності.
4.1. Обчислюється лінійна швидкість точки А кривошипа.
 ,
,
де ω 1 − кутова швидкість кривошипа:
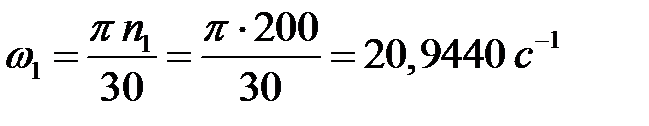 .
.
Вектор швидкості  направлений перпендикулярно до кривошипа ОА в бік обертання.
направлений перпендикулярно до кривошипа ОА в бік обертання.
4.2. Визначається масштаб плану швидкостей
 ,
,
де 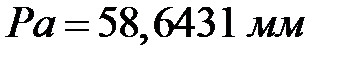 − довжина відрізка, що зображує вектор швидкості VA на плані швидкостей. Довжина відрізка Pa (мм) вибирається так, щоб розміри плану швидкостей всього механізму знаходилися в прийнятих межах.
− довжина відрізка, що зображує вектор швидкості VA на плані швидкостей. Довжина відрізка Pa (мм) вибирається так, щоб розміри плану швидкостей всього механізму знаходилися в прийнятих межах.
4.3. Визначається швидкість точки В. Точка В є спільною для ланок 2 і 3, тому її рух залежить від руху цих ланок одночасно.
а) Розглядаємо рух ланки 2. Вона здійснює плоскопаралельний рух, який можна подати таким, що складається з поступального руху зі швидкістю точки, прийнятої за центр обертання, і обертального руху навколо цього центра.
Приймаємо за центр обертання точку А і записуємо векторне рівняння:
 , (1)
, (1)
де 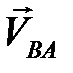 − швидкість, яку набуває точка В в обертанні навколо точки А;
− швидкість, яку набуває точка В в обертанні навколо точки А;
 .
.
б) Розглядаємо рух ланки 3. Вона здійснює зворотньо-коливальний рух. Приймаємо за центр обертання точку С і записуємо:
 , (2)
, (2)
де  = 0 – швидкість точки С;
= 0 – швидкість точки С;
 – швидкість, яку набуває точка В в обертальному русі ланки 3 навколо точки С;
– швидкість, яку набуває точка В в обертальному русі ланки 3 навколо точки С;
 .
.
Оскільки точка В належить коромислу 3, то її швидкість перпендикулярна ВС.
Швидкість  зображується на плані швидкостей відрізком
зображується на плані швидкостей відрізком  , швидкість
, швидкість  − відрізком
− відрізком  , а
, а  , так що рівняння (1) у відрізках плану запишеться
, так що рівняння (1) у відрізках плану запишеться
 . (1')
. (1')
Побудова плану швидкостей виконується в наступній послідовності. На площині вибираємо довільну точку – полюс Р. Від полюса Р відкладаємо перпендикулярно ОА в бік обертання відрізок  , який зображує в масштабі
, який зображує в масштабі 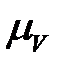 швидкість точки А кривошипа 1. Швидкість точки О (як і точки С) дорівнює нулю, тому відповідна точка о (с) на плані співпадає з полюсом Р.
швидкість точки А кривошипа 1. Швидкість точки О (як і точки С) дорівнює нулю, тому відповідна точка о (с) на плані співпадає з полюсом Р.
З кінця відрізка  , тобто з точки а, проводиться перпендикулярно до ланки АВ напрям відносної швидкості
, тобто з точки а, проводиться перпендикулярно до ланки АВ напрям відносної швидкості  , модуль якої ще невідомий.
, модуль якої ще невідомий.
Рівняння (2) у відрізках плану запишеться
 . (2')
. (2')
Згідно з останнім рівнянням в полюсі плану розташовується точка c (нуль-вектор швидкості точки С), а з цієї точки перпендикулярно до ланки ВС проводиться напрям швидкості 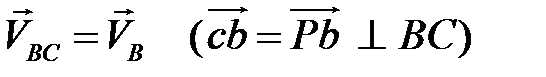 .
.
В перетині цих двох прямих розташована точка b, а відрізок Рb, проведений з полюса, зображує вектор швидкості  . Замірюємо довжину цього відрізка і визначаємо швидкість точки В:
. Замірюємо довжину цього відрізка і визначаємо швидкість точки В:
 .
.
Відносні швидкості:  ;
;
 .
.
4.4. Теорема подібності для планів швидкостей: план швидкостей ланки подібний їй і повернутий відносно неї на 900 у бік миттєвого обертання.
Швидкість точки D 2 (ланки АВ), з якою в даний момент співпадає повзун D, визначається за допомогою властивості подібності картини відносних швидкостей фігур і ланки (теорема подібності для планів швидкостей) і знаходиться із співвідношення:
 ,
,
звідки
 .
.
Значення AD 2 = 12,5588 мм береться безпосередньо з креслення (див. Плани положень механізма).
Відрізок Pd 2 , проведений з полюса плана в точку d 2, зображує вектор швидкості точки D 2. Його значення також береться з креслення (див. Плани швидкостей). Абсолютне значення швидкості
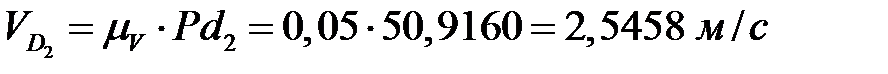 .
.
4.5. Швидкість точки D повзуна, який здійснює складний рух, дорівнює
 , (3)
, (3)
у відрізках плану  , (3')
, (3')
де  – відносна швидкість повзуна D при його ковзанні уздовж ланки АВ, яка має напрям паралельний АВ (
– відносна швидкість повзуна D при його ковзанні уздовж ланки АВ, яка має напрям паралельний АВ ( ).
).
Вектор абсолютної швидкості точки D, як і будь-якої точки ланки DЕ, направлений вздовж DЕ (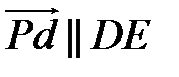 ).
).
Згідно з рівнянням (3) на плані швидкостей через точку d 2 проводиться пряма ( ), паралельна АВ, а через полюс плана – пряма (
), паралельна АВ, а через полюс плана – пряма ( ), паралельна DЕ. В перетині цих прямих розташована точка d. Промінь Pd зображує вектор швидкості точки D, а відрізок d 2 d – відносну швидкість
), паралельна DЕ. В перетині цих прямих розташована точка d. Промінь Pd зображує вектор швидкості точки D, а відрізок d 2 d – відносну швидкість  .
.
Абсолютне значення швидкостей:
 ;
;
 .
.
4.6. Кутові швидкості ланок.
Для шатуна АВ:  .
.
Для визначення напряму кутової швидкості  треба вектор відносної швидкості
треба вектор відносної швидкості  перенести подумки в точку В і спостерігати, в який бік цей вектор обертає ланку АВ відносно точки А. В нашому випадку, тобто в положенні II, кутова швидкість
перенести подумки в точку В і спостерігати, в який бік цей вектор обертає ланку АВ відносно точки А. В нашому випадку, тобто в положенні II, кутова швидкість  має напрям проти руху годинникової стрілки (див. креслення-вкладку).
має напрям проти руху годинникової стрілки (див. креслення-вкладку).
Кутова швидкість ланки ВС: 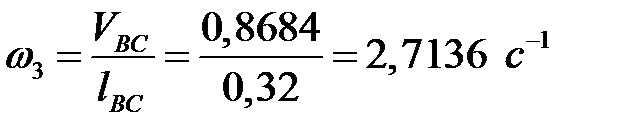 .
.
Точка В разом з ланкою 3 рухається навколо нерухомої точки С у напрямі швидкості  . У цьому випадку (для положення ІІ) коромисло ВС повертається за годинниковою стрілкою з кутовою швидкістю
. У цьому випадку (для положення ІІ) коромисло ВС повертається за годинниковою стрілкою з кутовою швидкістю  .
.
Кутова швидкість повзуна D співпадає з кутовою швидкістю ланки 2:
 .
.
Ланка 5 завжди рухається поступально, тому кутова швидкість плунжера DЕ:
 .
.
Значення лінійних швидкостей точок механізма та кутових швидкостей його ланок наведено в табл.1.
Таблиця 1
Швидкості точок механізма (в м/с)
та кутові швидкості його ланок (в с-1)
| Параметр | Положення кривошипа | |||
| I | II | III | ||

| 2,9322 | |||

| 1,6556 | 2,9305 | 0,8684 | 3,8003 |
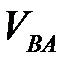
| 4,0483 | 0,0176 | 2,7242 | 1,2335 |
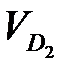
| 1,2694 | 2,9314 | 2,5458 | 3,4208 |

| 0,8004 | 0,2720 | 2,5059 | 3,0996 |

| 1,3037 | 2,9447 | 0,1257 | 4,2034 |
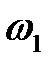
| 20,9440 | |||

| + 9,6389 | + 0,0418 | - 6,4861 | - 2,9368 |

| - 5,1738 | - 9,1579 | + 2,7136 | + 11,8759 |
Примітка. Знак ”+” відповідає напряму кутової швидкості проти руху годинникової стрілки, “-“ – за рухом годинникової стрілки.
5. Побудова планів прискорень
Побудова планів прискорень розглядається для II положення механізма (див. креслення-вкладку) і здійснюється в такій послідовності.
5.1. Кривошип ОА обертається рівномірно ( ). У цьому випадку прискорення точки А ланки 1 дорівнює її нормальному прискоренню (напрямлено до центра обертання О), тобто
). У цьому випадку прискорення точки А ланки 1 дорівнює її нормальному прискоренню (напрямлено до центра обертання О), тобто
 .
.
5.2. Визначається масштаб плану прискорень:
 ,
,
де  − довжина відрізка, що зображує вектор прискорення
− довжина відрізка, що зображує вектор прискорення  на плані прискорень. Його довжина вибирається за таким же принципом, як довжина відрізка
на плані прискорень. Його довжина вибирається за таким же принципом, як довжина відрізка  на плані швидкостей.
на плані швидкостей.
5.3. Визначається прискорення точки В. Точка В є спільною для ланок АВ і ВС, тому її рух залежить від руху цих ланок одночасно.
а) Розглядаємо рух ланки АВ. Вона здійснює плоскопаралельний рух. Приймаємо за центр обертання точку А і записуємо рівняння:
 , (4)
, (4)
де  та
та  − відповідно нормальне і тангенціальне прискорення точки В відносно точки А.
− відповідно нормальне і тангенціальне прискорення точки В відносно точки А.
Прискорення  зображується на плані прискорень відрізком
зображується на плані прискорень відрізком  ,
,  ,
,  , а
, а  , так що останнє рівняння у відрізках плану прискорень запишеться
, так що останнє рівняння у відрізках плану прискорень запишеться
 . (4')
. (4')
Визначаємо модулі векторів.
Нормальне (або доцентрове) прискорення  направлено від точки В до точки А і дорівнює
направлено від точки В до точки А і дорівнює
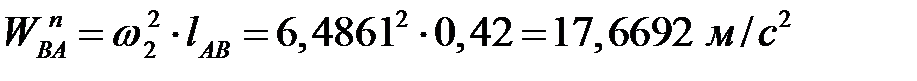 .
.
Довжина відрізка  , що зображує вектор цього прискорення на плані прискорень
, що зображує вектор цього прискорення на плані прискорень
 .
.
Тангенціальне (або дотичне) прискорення  має напрям перпендикулярний до ланки АВ і за модулем невідомо.
має напрям перпендикулярний до ланки АВ і за модулем невідомо.
б) Розглядаємо рух ланки ВС. Вона теж здійснює плоскопаралельний рух. Приймаємо за центр обертання точку С і записуємо рівняння:
 , (5)
, (5)
 , (5')
, (5')
де  та
та 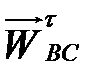 − відповідно нормальне і тангенціальне прискорення точки В відносно точки С.
− відповідно нормальне і тангенціальне прискорення точки В відносно точки С.
Визначаємо модулі векторів.
Прискорення  .
.
Нормальне прискорення  направлено від точки В до точки С і дорівнює
направлено від точки В до точки С і дорівнює
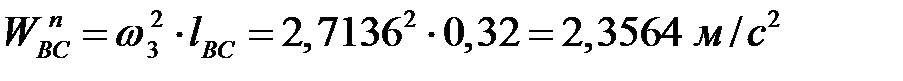 .
.
Довжина відрізка  , що зображує вектор цього прискорення на плані прискорень
, що зображує вектор цього прискорення на плані прискорень
 .
.
Тангенціальне прискорення 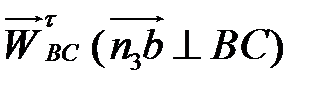 має напрям перпендикулярний до ланки ВС і за модулем невідомо.
має напрям перпендикулярний до ланки ВС і за модулем невідомо.
Побудова плану прискорень. На площині довільно вибираємо полюс  . Від нього відкладаємо відрізок
. Від нього відкладаємо відрізок  паралельно ОА, у напрямі від точки А до точки О. Оскільки прискорення точки О (як і точки С) дорівнює нулю, то відповідна точка о (с) співпадає з полюсом
паралельно ОА, у напрямі від точки А до точки О. Оскільки прискорення точки О (як і точки С) дорівнює нулю, то відповідна точка о (с) співпадає з полюсом  . Згідно з векторними рівняннями (4'), (5') від точки а відкладаємо в напрямі від В до А відрізок
. Згідно з векторними рівняннями (4'), (5') від точки а відкладаємо в напрямі від В до А відрізок  , а від полюса
, а від полюса  у напрямі від В до С відрізок
у напрямі від В до С відрізок  . З точки
. З точки  проводимо пряму, перпендикулярну АВ (
проводимо пряму, перпендикулярну АВ ( ), а з точки
), а з точки  − перпендикулярну ВС (
− перпендикулярну ВС ( ). На їх перетині знаходимо точку b.
). На їх перетині знаходимо точку b.
Модулі прискорень визначаються з плану:
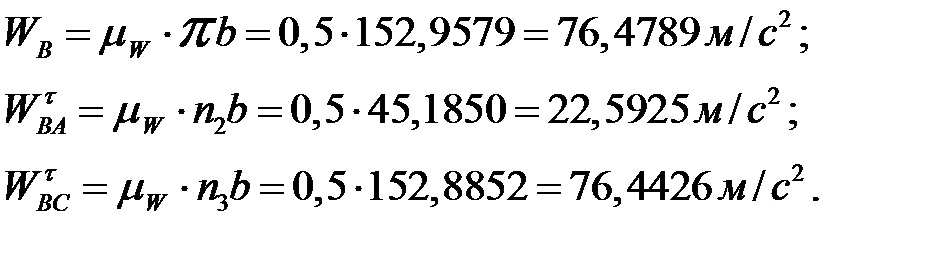
5.4 Теорема подібності для планів прискорень: план прискорень ланки подібний їй і повернутий відносно неї.
Прискорення точки D 2 (ланки АВ), з якою в даний момент співпадає повзун D, визначається за допомогою властивості подібності картини відносних прискорень фігур і ланки (теорема подібності для планів прискорень) і знаходиться із співвідношення:
 ,
,
звідки
 .
.
Значення AD 2 = 12,5588 мм береться безпосередньо з креслення (див. Плани положень механізма).
Відрізок 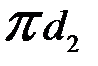 , проведений з полюса плану в точку d 2, зображує вектор прискорення точки D 2. Його значення береться з креслення (див. Плани прискорень). Абсолютне значення прискорення
, проведений з полюса плану в точку d 2, зображує вектор прискорення точки D 2. Його значення береться з креслення (див. Плани прискорень). Абсолютне значення прискорення
 .
.
5.5. Прискорення точки D повзуна, який здійснює складний рух, визначається за теоремою Коріоліса:

 , (6)
, (6)
 , (6')
, (6')
де 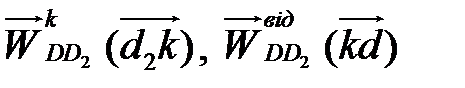 − прискорення Коріоліса та відносне прискорення точки D повзуна відносно D 2 ланки 2.
− прискорення Коріоліса та відносне прискорення точки D повзуна відносно D 2 ланки 2.
Коріолісове прискорення
 .
.
Відрізок  , що зображує коріолісове прискорення
, що зображує коріолісове прискорення  на плані прискорень
на плані прискорень
 .
.
Вектор коріолісового прискорення має напрям вектора відносної швидкості  , попередньо повернутого в бік переносної кутової швидкості
, попередньо повернутого в бік переносної кутової швидкості  на 90º. В положенні ІІ, яке розглядається, вектор коріолісового прискорення
на 90º. В положенні ІІ, яке розглядається, вектор коріолісового прискорення  має напрямок перпендикулярно до ланки АВ униз.
має напрямок перпендикулярно до ланки АВ униз.
Відносне прискорення  має напрям вздовж ланки АВ і за модулем невідомо.
має напрям вздовж ланки АВ і за модулем невідомо.
Абсолютне прискорення  точки D, як точки, що належить ланці DЕ, має напрям вздовж неї (поступальний рух), тобто вертикальний.
точки D, як точки, що належить ланці DЕ, має напрям вздовж неї (поступальний рух), тобто вертикальний.
Згідно з рівнянням (6') з точки d 2 відкладається відрізок  , що зображує коріолісове прискорення
, що зображує коріолісове прискорення  , через точку k проводиться паралельно ланці АВ лінія дії відносного прискорення
, через точку k проводиться паралельно ланці АВ лінія дії відносного прискорення 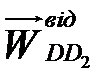 , а через полюс плану – пряма, паралельна DЕ. В перетині одержується точка d. З’єднуючи точку d з полюсом плану, отримують відрізок
, а через полюс плану – пряма, паралельна DЕ. В перетині одержується точка d. З’єднуючи точку d з полюсом плану, отримують відрізок  , що зображує абсолютне прискорення точки D.
, що зображує абсолютне прискорення точки D.
Модуль прискорення  .
.
5.6. Кутові прискорення ланок.
Кутове прискорення ланки АВ:  .
.
Для визначення напряму кутового прискорення  точку В разом з шатуном 2 повертаємо уявно навколо нерухомої у відносному русі точки А в напрямі тангенціального прискорення
точку В разом з шатуном 2 повертаємо уявно навколо нерухомої у відносному русі точки А в напрямі тангенціального прискорення 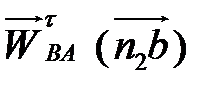 . Одержаний для даного положення механізму уявний напрям обертання проти стрілки годинника визначає напрямок
. Одержаний для даного положення механізму уявний напрям обертання проти стрілки годинника визначає напрямок  .
.
Аналогічно отримуємо кутове прискорення ланки ВС:
 .
.
Напрямок 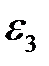 − за рухом годинникової стрілки.
− за рухом годинникової стрілки.
Кутове прискорення ланок 2 і 4 однакові:  .
.
Ланка 5 рухається поступально, тому  .
.
Значення прискорень точок і кутових прискорень ланок для всіх положень механізма наведені в табл. 2.
Таблиця 2
Прискорення точок механізма (в м/с2) та
кутові прискорення його ланок (в с-2)
| Параметр | Положення кривошипа | |||
| І | ІІ | ІІІ | ||

| 61,4109 | |||

| 39,0213 | 0,0007 | 17,6692 | 3,6224 |

| 11,7715 | 88,6012 | 22,5925 | 18,2953 |

| 40,7582 | 88,6012 | 28,6814 | 18,6505 |

| 8,5659 | 26,8376 | 2,3564 | 45,1318 |

| 19,0618 | 8,2764 | 76,4426 | 3,8462 |

| 20,8980 | 28,0848 | 76,4789 | 45,2954 |

| 26,3659 | 19,6389 | 63,0661 | 51,6337 |

| 25,1330 | 0,2462 | 1,6310 | 24,6891 |

| 18,6673 | 4,0776 | 66,3729 | 12,4560 |

| 14,7841 | 18,5864 | 17,1296 | 78,6517 |

| - 28,0273 | - 210,9551 | + 53,7916 | + 43,5602 |

| + 59,5680 | + 25,8636 | - 238,8832 | - 12,0195 |
Примітка. Знак ”+” відповідає напряму кутового прискорення проти руху годинникової стрілки, “-“ – за рухом годинникової стрілки.
Дата добавления: 2015-08-17; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В задачах інженерної механіки | | | Основні елементи вікна AutoCAD |