Глава 8. Теория цен Фарджуна и Маховера

Когда Шайк и другие эмпирические исследователи начали в 1984 году публиковать свои результаты, последние стали сюрпризом для экономистов, которые обратили на них внимание. Но годом раньше появилась знаменательная книга «Законы хаоса» (Фарджун и Маховер, 1983). В книге, написанной двумя физиками, доказывалось, что экономисты ошибаются, пытаясь сконструировать полностью детерминистские теории. Авторы указывали, что еще начиная с Больцмана, физики могли делать полезные предсказания об общем поведении систем, которые в малом масштабе кажутся случайными и хаотическими.

В малом масштабе движение молекул газа или жидкости случайно, и это случайное движение можно даже, как указал в 1905 году Эйнштейн, увидеть в форме броуновского движения — наблюдаемых под микроскопом колебаний маленьких частичек, например, пыльцы, в воде. Но в большом масштабе эти случайные движения усредняются, что позволяет делать полезные обобщения: законы газа, законы термодинамики. Фарджун и Маховер утверждали, что экономисты застряли в модели причинности образца начала XIX века. Если ее оставить, то становятся возможными несколько различных способов рассуждений об экономике. Практически полностью обойдясь без ортодоксальных экономических теорий, авторы вывели несколько интересных обобщений о работе капиталистических экономик. Одним из них было предсказание тесной корреляции рыночных цен с трудовыми стоимостями.

В науке предсказания всегда более убедительны, чем «послесказания». Тот факт, что теоретические результаты Фарджуна и Маховера были вскоре подтверждены эмпирическими исследованиями, придало им вес, особенно, если учесть, что предсказания совершенно противоречили общепринятым в экономике мнениям Мы вряд ли сможем полностью изложить их теорию в нашей работе. Поэтому мы расскажем о ней упрощенно, опустив почти всю математическую строгость, но достаточно для интуитивного понимания механизма, который они предложили в качестве объяснения закона стоимости.

Рассмотрим все товары, проданные фирмами одной страны в течение недели. Это будет длинный список товаров и услуг, дорогих и дешевых. Некоторые требуют для своего производства большое количество труда, некоторые — нет. Предположим, что закон стоимости действует и цены товаров примерно пропорциональны содержанию в них труда. Как мы можем это измерить?

Фарджун и Маховер ввели случайную переменную Ψ, которая означает среднюю цену труда в течение часа. Идея состоит в том, что мы выражаем все производство различных товаров: аэробусов А380, шоколадных бисквитов, одноразовых носовых платков и т.д. в терминах содержания в них труда. Затем мы делим его на единицы по часу каждая и представляем, что случайно выбираем часы из этого огромного списка. Затем мы смотрим, чему соответствуют эти часы, выраженные в деньгах.

Ученые предсказали, что если изобразить частоту различных значений Ψ, наблюдаемую на достаточно большой выборке товаров, тогда распределение будет выглядеть так, как на рис. 8.1. Оно должно принять форму колоколообразной кривой, соответствующей тому, что статистики называют нормальным распределением.

Рис. 8.1. Предсказанная Фарджуном и Маховером форма связи Ψ между трудовой стоимостью и ценой

Нормальное распределение, как указывает само его название – это одно из наиболее часто встречающихся видов распределения. Многие наблюдения воплощаются в такой форме. Например, если нарисовать на графике высоту десятилетних мальчиков из Лондона, то получится нормальное распределение. Если нарисовать тщательно измеренный вес достаточно большого количества одинаковых монет, получится нормальное распределение. Если нарисовать количество фотонов, приходящих за секунду в телескоп с какой-нибудь удаленной звезды, получится нормальное распределение. Собственно, всегда, когда величина, которую измеряют, является результатом сложения большого количества случайных независимо действующих причин, распределение, которое получится на графике, будет знакомой колоколообразной кривой нормального распределения.

Нормальное распределение N(μ,σ) характеризуется двумя числами: математическим ожиданием (μ), характеризующим вершину распределения, и стандартным отклонением (σ), описывающим ширину колокола кривой. Фарджун и Маховер предсказали, что график зависимости цен от трудовых стоимостей будет иметь матожидание 2 и стандартное отклонение, меньшее 1/3. Как они пришли к такому выводу?

Во-первых, почему они утверждают, что матожидание равно двум, то есть средняя цена товара будет в два раза выше его трудовой стоимости?

Частично это зависит от выбранной ими единицы измерения. Как только вы попытаетесь создать теорию цен, перед вами станет вопрос единицы расчетов. Когда мы хотим измерить расстояние, мы можем воспользоваться метрами, которые, в свою очередь, определены в терминах естественных констант – длины волны определенного света. С их помощью получается стандарт, не зависящий от пространства и времени. Но чем мы можем измерить цены?

Если мы используем деньги, то должны это быть доллары, евро или йены?

Если мы будем применять одну из валют, как мы сможем учесть инфляцию?

Чтобы решить эту проблему, Фарджун и Маховер используют технику, одобренную Адамом Смитом и Мейнардом Кейнсом. Они используют как единицу измерения среднюю часовую зарплату. Смит, как мы видели, считал, что настоящей ценой любого товара является количество труда, которое он получает в свое распоряжение. Фарджун и Маховер были чуть-чуть точней и определили действительную цену товара, для производства которого требуется час труда, как количество часов труда, оплачиваемых по средней часовой ставке, которыми он может распоряжаться. Предположим, что четыре килограмма трески для доведения до товарной кондиции требуют часа прямого и косвенного труда. Предположим также, что эту треску можно продать за 15 фунтов, а средняя часовая ставка равна 6 фунтам. В терминологии Фарджуна и Маховера:

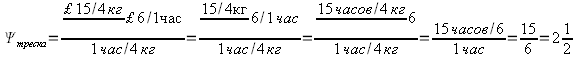
Мы можем ожидать, что Ψ будет >1, поскольку продажную цену товара можно, как показал Смит, разложить на зарплату и прибыль 4. Продажная цена уходит на выплату зарплаты, прибыль и издержки на сырье. Но стоимость сырья можно точно также разложить на зарплаты, прибыль и стоимость сырья. Если вы будете двигаться все дальше и дальше, то обнаружите, что конечная доля сырья стремится к нулю, поэтому можно сказать, что вся продажная цена в конце концов делится на зарплату и прибыль 5.. Поскольку Фарджун и Маховер сочли, что в большинстве капиталистических стран добавленная стоимость распределяется между зарплатой и прибылью поровну, отсюда следует, что средняя цена продукта в рабочих часах будет в два раза выше средней стоимости часа труда.

Это объясняет, почему они считают, что матожидание равно 2. Почему они определяют стандартное отклонение равным 1/3?

Доказательство очень простое. Они указывают, что товары очень редко продаются так дешево, что продажной цены будет недостаточно для уплаты прямой и косвенной зарплаты, необходимой для их производства. Граница проходит при значении Ψ = 1. Кроме этого, производство товара будет невыгодным, если оно не покрывает расходов даже на прямую зарплату. Они предполагают, что существует только один шанс из тысячи, что товар будет продаваться дешевле стоимости своего производства.

Посмотрев в таблицу нормального распределения, можно узнать, что вероятность того, что отклонение от средней составит 3 стандартных отклонения, равна около 1/1000, отсюда они выводят, что , поэтому для μ равного двум,? должно быть равно 1/3.

Как эти предсказания соотносятся с реальными данными? Используя данные по Англии за 1984 год – год после выхода книги Фарджуна и Маховера – мы рассчитали 6, что Ψ хорошо ложится в распределение с μ=1,46 и σ = 0,151.

На первый взгляд, результаты сильно отличаются от предсказанных. Но разница почти целиком объясняется тем фактом, что в 1984 году в Великобритании добавленная стоимость распределялась между прибылью и зарплатами в соотношении один к двум вместо равного, предполагаемого Фарджуном и Маховером. Полная форма их предсказания имеет следующий вид: если e есть отношение агрегатной прибыли к агрегатной зарплате, то при и . Если мы подставим правильное значение e в данные для Великобритании 1984 года, то получим почти точное соответствие.

Из этой теории вытекает интересное следствие: связь между ценами и трудовыми стоимостями будет сильнее, когда доля прибыли в национальном доходе меньше. Если доля прибыли в национальном доходе уменьшается, тогда можно ожидать, что относительные рыночные цены будут больше приближаться к относительным трудовым стоимостям. Из-за прибыли отношение сигнала к шуму для цен увеличивается.

Распределение Ψ случайно или энтропийно. Можно рассчитать энтропию нормально распределенной случайной переменной, применяя модифицированную формулу Шеннона. Шеннон определял энтропию сигнала как

где i принимает набор дискретных величин, соответствующих различным различимым состояниям сигнала. Нормальное распределение N(?,?) – это плотность вероятности. Это функция, определенная на поле действительных чисел, такая что

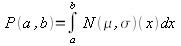
определяет вероятность того, что x будет находиться в интервале a..b. Если мы подставим ее в формулу Шеннона и численно проинтегрируем, то сможем рассчитать энтропию нормального распределения при заданном стандартном отклонении.

Мы обнаружили таким образом, что нормальные распределения с малым стандартным отклонением обладают низкой энтропией, а с большим отклонением – высокой энтропией. На рисунке 8.2 показано распределение Ψ, предсказанное Фарджуном и Маховером, а рядом для сравнения нормальное распределение с математическим ожиданием и стандартным отклонением, наблюдавшимся в Великобритании в 1984 году. Энтропия более широкой кривой справа около 7,1 битов, той, что слева, - около 5,9 битов.

Дата добавления: 2015-08-18