Escape velocity of an object

Escape velocity as needed in order to find the minimum velocity at which the satellite will overcome the force of gravity of the planet and get away from the orbit, without having chance to return. Due to the fact that the gravity is a force of attractive and using Newton’s law of Gravitation Pull: and using Newton’s Second Law , where is acceleration. The formula become , and after cancelling out values of , the formula 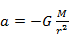is obtained.

Since that acceleration ( is the derivative of velocity, which is mean that , furthermore velocity is the derivative of radius, means that . Using chain rule to the equations above . Substitute that value to equation , is obtained that , then after doing work with that equation getting new equation, which is , that equation should be integrated to find the value of velocity. Before integration is carried out, the value where will be integrated, the result should be between 0 and v, because from integration is used to get the velocity. While for it is the value from center of planet until surface () to infinity, because purpose is to find value of velocity when satellite will get away from orbit.

Making function from above information:

Thus 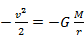give to us the final formula, where .

From this formula the value of velocity for each planet can be easily obtained, finished only derive the final formula for velocity. Hence last formula:

this is the formula for escape velocity. Finding escape velocity to each planet:

for Planet A:

which is equal

for Planet B:

which is equal .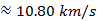

Hence from results, it is possible to say that here mass of planet and including radius are influences to escape velocity of an object.

Дата добавления: 2015-08-18