Orbital Velocity of a satellite

This part includes an explanation on how the masses of the planets affect the orbital velocity of satellite which will move around planets orbit. To find orbital velocity of a satellite the formula below can be used:

Newton’s Law of Gravitation Pull: , this is where 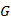is a gravity constant, 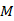is the mass of the planet, is the mass of the satellite and is the distance from center of the planet to the satellite (. Since satellite moving around the planet, the motion of satellite is circular. Hence; an object have acceleration, which could be shown like 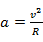. Using Newton’s Second Law: , can be substitute by and the formula become 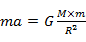. Therefore, it can be assumed that the satellite have acceleration in uniform circular motion, substitute to . So the formula become , because we have value and in both sides, they could be excluded: , if took square root from both sides, find a formula for calculating orbital velocity of a satellite: 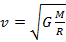. By the condition value of height of satellite is equal to and mass is equal to 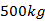. Substitute the values ​​in its place, finding value of orbital velocity of a satellite.

For Planet A: , which is .

For Planet B: , which is .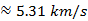

Based on the results, it is possible to say that the orbital velocity of a satellite is completely dependent on the mass of the planet. This means, the greater the mass of the planet, the greater the gravity pulls an object. Therefore, to make satellite be on an orbit of a planet it should have big velocity.

Дата добавления: 2015-08-18