Projectile Motion

The motion of the projectile includes a situation where an object with constant mass, running at a speed of 100 m/s and at an angle of 45 degrees on the two planets and see where object flew a more distance. The projectile motion on the planets depends on gravity. The formula for calculating the gravity can be obtained from Newton’s law of Gravity Pull, where ( 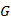is a constant value of ). Using Newton’s second law can be replaced with , therefore . The acceleration can be replaced by gravity, since gravity change the velocity , the mass of the projectile can be cancelled. Therefore, we can obtain the value of gravity on both planets with using the formula . We substitute the values ​​of the mass and radius of the two planets from the formula . The gravity of Planet A is 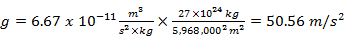and Planet B is . The following calculations will determine the change of the projectile motion on two planets horizontally and vertically. To get the value of changing horizontal displacement the formula can be applied. To obtain the vertical displacement value the formula 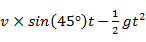can be applied. These formulas will be used to obtain the values of each planets gravity.

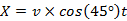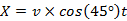For easy location, displacement can be represented as a function on Y and X axes, for Planet A is and , for Planet B is and .

Using Microsoft Excel and the formulas above, the value of horizontal and vertical displacement can be shown in forms of table and graph.

Table 1: Vertical and Horizontal Displacement

Time (s)	Vertical DisplacementA and B (m)	Horithontal DisplacementA (m)	Horithontal DisplacementB (m)
0.00	0.00	0.00	0.00
0.50	35.36	29.03	34.65
1.00	70.71	45.43	67.87
1.50	106.07	49.18	99.68
2.00	141.42	40.30	130.06
2.50	176.78	18.77	159.03
3.00	212.13	-15.40	186.57
3.50	247.49	-62.21	212.69
4.00	282.84	-121.66	237.40
4.50	318.20	-193.75	260.68
5.00	353.55	-278.48	282.55
5.50	388.91	-375.86	302.99
6.00	424.26	-485.87	322.02
6.50	459.62	-608.52	339.62
7.00	494.97	-743.82	355.80
7.50	530.33	-891.75	370.57
8.00	565.69	-1052.33	383.91
8.50	601.04	-1225.54	395.83
9.00	636.40	-1411.40	406.34
9.50	671.75	-1609.90	415.42
10.00	707.11	-1821.04	423.08
10.50	742.46	-2044.82	429.33
11.00	777.82	-2281.24	434.15
11.50	813.17	-2530.30	437.55
12.00	848.53	-2792.00	439.54
12.50	883.88	-3066.34	440.10
13.00	919.24	-3353.33	439.24
13.50	954.59	-3652.95	436.96
14.00	989.95	-3965.21	433.27
14.50	1025.30	-4290.12	428.15
15.00	1060.66	-4627.67	421.61
15.50	1096.02	-4977.85	413.65
16.00	1131.37	-5340.68	404.27
16.50	1166.73	-5716.15	393.48
17.00	1202.08	-6104.26	381.26
17.50	1237.44	-6505.01	367.62
18.00	1272.79	-6918.40	352.56
18.50	1308.15	-7344.43	336.08
19.00	1343.50	-7783.10	318.18
19.50	1378.86	-8234.41	298.86
20.00	1414.21	-8698.37	278.13
20.50	1449.57	-9174.96	255.97
21.00	1484.92	-9664.20	232.39
21.50	1520.28	-10166.07	207.39
22.00	1555.63	-10680.59	180.97
22.50	1590.99	-11207.74	153.13
23.00	1626.35	-11747.54	123.87
23.50	1661.70	-12299.98	93.19
24.00	1697.06	-12865.06	61.09
24.50	1732.41	-13442.78	27.57
25.00	1767.77	-14033.14	-7.37

The table 1 shows the movement of a projectile on the two planets. The maximum vertical and horizontal displacements of projectile on Planet A are and , while on Planet B maximum vertical and horizontal displacements are 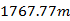and . The result of the calculations can vary, depends on the time as the position of the projectile depends from time.

Graph 1: Displacement of projectile

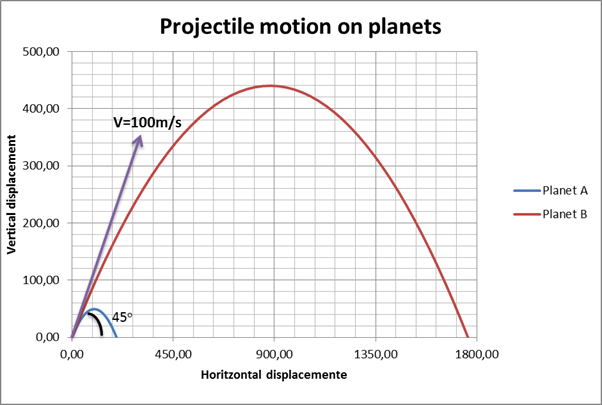
This graph above gives a visual indication of the change in position of the projectile on each planet. Also, it shows the maximum height to which the projectile rose and the maximum path traversed by the object on each planet. Based on the calculation where gravity on Planet A is and gravity on Planet B is (can be seen that gravity on Planet A is ten times more that on Planet B) and it is also shown in Graph 1, it is safe to say that projectile on Planet A travelled less distance than on Planet B. The maximum value of vertical displacement on Planet A is , horizontal is . While the maximum value of vertical displacement on Planet B is , horizontal is . 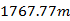Based on materials above is possible to say that gravity affects the projectile motion.

Дата добавления: 2015-08-18