Диаграмма состояния влажного атмосферного воздуха

Характеристики влажного воздуха можно определять по диарамме, предложенной в 1917 году профессором Л.К.Рамзиным (рис.1). Диаграмма I-х выражает зависимость между энтальпией I, [кДж/кг с.в.] и влагосодержанием х, [кДж/кг с.в.] воздуха. Диаграмма построена для 1 кг сухого воздуха при давлении Р = 745 мм рт.ст. Угол между координатными осями выбран 135°. Для удобства расчетов на диаграмме нанесена вспомогательная ось влагосодержаний х, проведенная под углом 90°.

В диаграмме, предложенной Л.К.Рамзиным, диаграмме I -d размерность влагосодержания воздуха d [г/кг с.в.], а энтальпию (теплосодержание) I вычисляли в [ккал/кг с.в.]. В международной системе единиц (СИ) массу принято измерять в килограммах массы, а энергию (тепло) в джоулях, поэтому впоследствии значения I и d Пересчитаны по уравнениям (1)-(2).

Рис.1 Диаграмма Рамзина.

На диаграмме построены линии постоянного влагосодержания (х = const), представляющие собой вертикальные прямые, параллельные оси ординат; нанесены линии постоянных температур или изотермы (t =const), линии постоянных энтальпий (I=const), прямые параллельные оси абсцисс (т.е. идущие под углом 135°С), при заданных х, t определены по уравнению (2).

В зависимости от влагосодержания х на основании уравнения (1) построена вспомогательная линия парциальных давлений пара р_п.

Воздух при одном и том же влагосодержании х, или р_п, но при разных температурах имеет различную относительную влажность . Она уменьшается при увеличении температуры, так как с увеличением температуры увеличивается упругость насыщенного пара π. При постоянной температуре φ растет при повышении влагосодержания х, так как при этом увеличивается Р_п. Следовательно, изменяя одновременно х иt, можно получить ряд точек, соответствующих φ= const.

На диаграмме I-х линии постоянной относительной влажности φ=const образуют пучок кривых, cходящихся в одну точку на оси ординат х=0. Кривая φ – 100%, соответствующая насыщенному состоянию воздуха при данной температуре, делит диаграмму на две части. Выше линии насыщения находится область ненасыщенного состояния влажного воздуха. Ниже линии насыщения находится область пересыщенных состояний (в технике сушки нереальных). Линии φ=const выше t = 99,6°С (температуры кипения воды при Р = 745 мм рт.ст.) идут вертикально по линии х = const.

На диаграмму I -х нанесены также линии, соответствующие состояниям воздуха при одной и той же температуре адиабатического насыщения, т.е. при одной и той же теоретической температуре "мокрого" термометра t_мт = const.

Если бы температура "мокрого" термометра равнялась 0°С, то процесс адиабатического насыщения протекал бы по линии I=const, так как при этом сколько физического тепла охлаждающийся воздух отдает воде, столько же тепла он получает с паром испарившейся воды в виде теплоты испарения. поскольку температура "мокрого" термометра больше 0°С, то, по мере испарения влаги, энтальпия воздуха увеличивается за счет присоединения физического тепла жидкости, превращенной в пар, т.е.

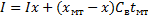(3)

где I - энтальпия при влагосодержании х;

Сp - теплоемкость воды.

По этому уравнению могут быть построены линии, соответствующие состояниям воздуха, имеющим одну и ту же теоретическую температуру "мокрого" термометра (рис.2). Проводя линию I=const из точки A (t_мт,x_мт) на рис.2 до пересечения с осью ординат, получаем точку В. При х=х_мтIx=I; при х=0 I-I=х_мтC_вt_мт. Откладывая из точки В вниз отрезок, равный х_мт С_вt_мт, получаем точку С. Прямая, соединяющая точки С и А (пунктирная), и будет линией t_мт =const. Как видно, энтальпия воздуха увеличивается пропорционально влагосодержанию, т.е. количеству испаряющейся воды в процессе насыщения.

2.3. Изображение на диаграмме I -х процессов сушки

Изображение на диаграмме I -х теоретического процесса сушки дано на рис.3, реального - на рис.4.

Для построения изображения теоретического процесса сушки на I -х диаграмме (рис.3) должны быть заданы характеристики атмосферного воздуха в точке А (t₀ и φ₀ или t₀ и t_мт) и еще две характеристики воздуха: (t₁,t₂), или (t1, φ₂), или (φ₂, t2), необходимые для определения положения точек В и С. Например, если заданы точки А и В, то находят А, проводят вертикаль АВ (до пересечения с изотермой t₁ ), изображающую процесс подогрева воздуха в калорифере при х₀. Из точки В по линии I=const проводят прямую ВС, изображающую процесс сушки до пересечения с t₂или φ₂. В теоретической сушилке испаряемая из материала влага вносит в воздух ровно столько тепла, сколько воздух отдает, охлаждаясь, на испарение влаги. Точка С характеризует свойства воздуха, покидающего сушилку. Уравнение теплового баланса теоретической сушилки I₁=I₂. Удельный расход воздуха l и тепла q (отнесенные на 1 кг испаренной влаги) в ней

(4)

Уравнение теплового баланса реальной сушилки:

, (5)

Где . (6)

Дата добавления: 2015-08-17