Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Вывод уравнения. Нормальный вектор плоскости. Общее уравнение плоскости.

Пусть P (x, y, z) — произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор
MP = { x − x ₀, y − y ₀, z − z ₀} ортогонален вектору

→

n

= { A, B, C } (рис.1).

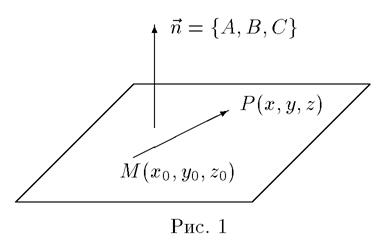
Написав условие ортогональности этих векторов (

n

MP) = 0 в координатной форме, получим:

A (x − x 0) + B (y − y 0) + C (z − z 0) = 0

(1)

Это и есть искомое уравнение. Вектор

→

n

= { A, B, C } называется нормальным вектором плоскости.

Таким образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор плоскости и какую–нибудь точку, принаждежащую плоскости.

Если теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:

Ax + By + Cz + D = 0,

где D = − Ax ₀ − By ₀ − Cz ₀.

Уравнение плоскости, проходящей через данную точку параллельно заданным векторам. Вывод уравнения. Уравнения прямой проходящей через 3 различные точки, не лежащие на одной прямой. Вывод уравнения

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, в ней

задана плоскость 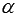и точка 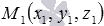, не лежащая в плоскости 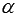. Поставим перед собой задачу: написать уравнение плоскости 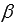, проходящей через точку 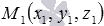параллельно плоскости 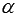.Решим ее.

Нам известно, что общее уравнение плоскости, проходящей через точку 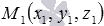и имеющей нормальный вектор плоскости 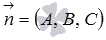, имеет вид 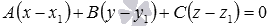. Таким образом, мы сможем записать требуемое уравнение плоскости 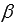, если определим координаты ее нормального вектора.

При изучении темы «нормальный вектор плоскости» мы отметили, что нормальный вектор одной из двух параллельных плоскостей является нормальным вектором второй плоскости. Следовательно, в силу параллельности плоскосте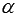й и 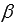, нормальным вектором плоскости 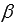является любой нормальный вектор заданной плоскости 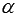. Таким образом, задача составления уравнения плоскости 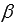, проходящей через заданную точку М1 параллельно заданной плоскости 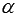, сводится к определению координат нормального вектора плоскости 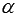. В свою очередь координаты нормального вектора плоскости 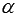проще всего получить, если иметь перед глазами общее уравнение плоскости 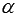вида 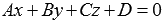. В этом случае коэффициенты A, B, C перед переменными x, y, z являются соответствующими координатами нормального вектора плоскости .

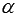Итак, запишем алгоритм нахождения уравнения плоскости 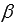, проходящей через заданную точку 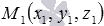параллельно заданной плоскости :

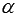получаем общее уравнение плоскости 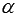в виде 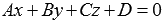(если оно нам уже не дано в условии) и записываем ее нормальный вектор ;

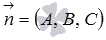принимаем этот вектор в качестве нормального вектора плоскости ;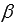

записываем уравнение плоскости, проходящей через точку 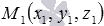и имеющей нормальный вектор 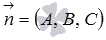, в виде 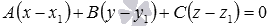- это и есть искомое уравнение плоскости 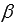, проходящей через заданную точку параллельно заданной плоскости.

Следует заметить, что если точка М1 лежит в плоскости 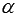, то, действуя по записанному алгоритму, мы получим уравнение плоскости 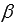, которая совпадает с плоскостью .

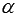Прежде чем приступать к составлению уравнения плоскости, проходящей через три заданные точки пространства, вспомним одну аксиому: через три несовпадающие и не лежащие на одной прямой точки трехмерного пространства проходит единственная плоскость. Таким образом, задав три различных и не лежащих на одной прямой точки, мы в трехмерном пространстве однозначно определим плоскость, проходящую через эти точки.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, в ней заданы три несовпадающие точки 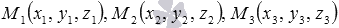, которые не лежат на одной прямой. Поставим перед собой следующую задачу: написать уравнение плоскости, проходящей через эти три точки.

Покажем два способа ее решения.

Первый способ составления уравнения плоскости, проходящей через три заданные точки .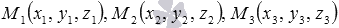

Известно, что общее уравнение плоскости вида 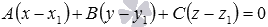задает в прямоугольной системе координат Oxyz плоскость 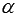, которая проходит через точку 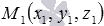, а нормальный вектор плоскости 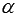имеет координаты 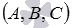. Следовательно, мы можем составить общее уравнение плоскости, если знаем координаты точки, через которую она проходит, и координаты нормального вектора этой плоскости. От этого знания и будем отталкиваться при нахождении уравнения плоскости, проходящей через три заданные точки .

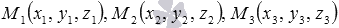Итак, из условия задачи нам известны координаты точки (даже координаты трех точек), через которую проходит плоскость, уравнение которой нам требуется составить. Осталось отыскать координаты нормального вектора 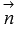этой плоскости.

Так как нормальный вектор плоскости и любой ненулевой вектор этой плоскости перпендикулярны, то вектор 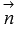перпендикулярен как вектору 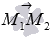, так и вектору 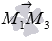. Следовательно, в качестве вектора 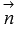можно принять векторное произведение векторов 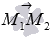и 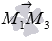. Так как 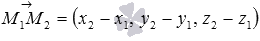и 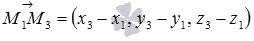(при необходимости обращайтесь к статье вычисление координат вектора по координатам точек), то 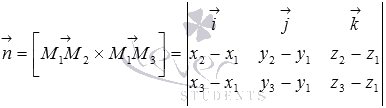. После вычисления записанного определителя, станут видны координаты нормального вектора 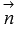, и можно записывать требуемое уравнение плоскости, проходящей через три заданные точки.

Второй способ нахождения уравнения плоскости, проходящей через три заданные точки .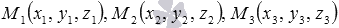

Очевидно, что множество точек 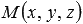определяет в прямоугольной системе координат Oxyz в трехмерном пространстве плоскость, проходящую через три различные и не лежащие на одной прямой точки 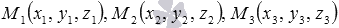, тогда и только тогда, когда три вектора 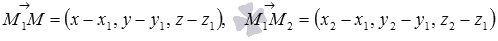и 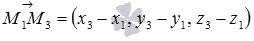компланарны.

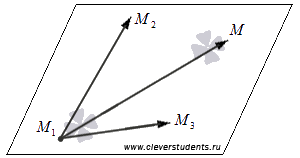
Следовательно, должно выполняться условие компланарности трех векторов 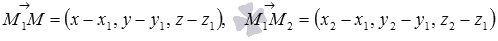и 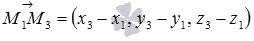, то есть, смешанное произведение векторов 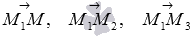должно быть равно нулю: 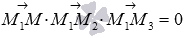. Это равенство в координатной форме имеет вид 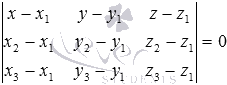. Оно, после вычисления определителя, представляет собой общее уравнение плоскости, проходящей через три заданные точки .

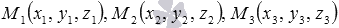Далее, от полученного общего уравнения плоскости, проходящей через три заданные точки, Вы при необходимости можете перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости.

Дата добавления: 2015-08-17