Метод решения задачи

Задача

Построить картину плоскопараллельного электрического поля, создаваемого двумя параллельными бесконечно длинными цилиндрами, несущими одинаковые по величине и различные по знаку заряды. Определить максимальный gradU в данной задаче, по картине поля найти емкость между цилиндрами на единицу длины и сравнить результаты с данными, полученными расчетным путем.

Исходные данные:

R₁=1см

R₂=1.5см

U=1200 В

т=12

D=10см

При построении картины поля, разность потенциалов между двумя соседними линиями должна быть всюду одинаковой (1200/12=100 В), а форма ячеек сетки, образованной линиями равного потенциала и силовыми линиями, должна быть близка к квадратной.

Метод решения задачи

По теореме единственности решения уравнения Лапласа, удовлетворяющего заданным граничным условиям, поле, ограниченное эквипотенциальными поверхностями, не изменится, если эти поверхности станут проводящими. Любая эквипотенциальная поверхность может быть заменена тонким проводящим листом, не изменяющим поля по обе стороны листа. В нашей задаче возможно расположить оси линейных проводов так, чтобы в их поле две поверхности равного потенциала совпали с поверхностями заданных проводящих цилиндров.

Рассмотрим поле двух заряженных одинаково по модулю нитей, расположенных симметрично относительно оси jy.

Комплексный потенциал в точке М(х, у) в этом случае выглядит так:

Переходя к показательной форме представления комплексных чисел 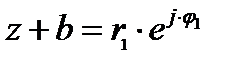и , получим для функции потока и потенциала выражения:

Положим 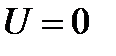при , тогда , аналогично при , так что и . Тогда:

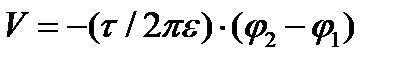
Нас будет интересовать форма линий потока и равного потенциала.

Уравнение линий равного потенциала , соответствует условию , тогда будет справедливо:

Путем несложных преобразований можно получить уравнение окружности:

Это окружность с координатами центра и радиусом .

Условие постоянного приращения потенциала при переходе к соседней линии равного потенциала:

, что равносильно условию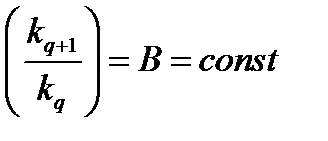

Уравнение любой линии напряженности – это дуга окружности:

Если , то видно, что годограф, подчиненный данному условию описывает окружность с координатами центра

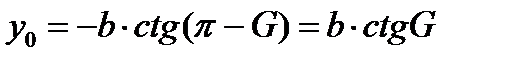
Далее, если обозначить - расстояние от любого из зарядов («электрической оси») до линии 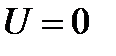, то будем иметь:

и 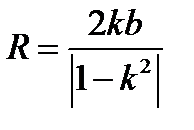, так что можно найти :

Исходя из этого, можно определить расстояния от осей цилиндров до линии :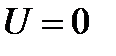

и также ,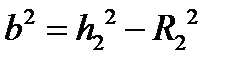

Получаем:

Дата добавления: 2015-08-17