Решение задачи

3.1. Нахождение расстояний от 1-ой и от 2-ой нитей до линии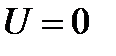

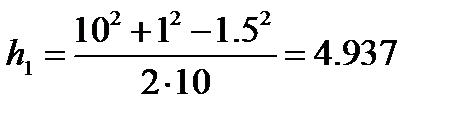см

см

см

см

или см

3.2. Вычисление параметров k для окружностей равного потенциала, являющихся основаниями цилиндров.

Для этого достаточно решить уравнения:

и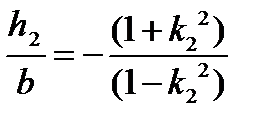

Решение первого:

Решение второго:

Также можно было вычислить и 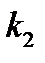по другим формулам (сходство в данном случае будет приближенным):

3.3. Вычисление линейных зарядов, потенциалов цилиндров, изменение угловой координаты.

Потенциалы цилиндров:

Поскольку для функций U и V шаг изменения равен 100 В (это вытекает из того что они являются мнимой и действительной частями аналитической функции W), то необходимо задать соответствующее изменение угловой координаты:

Теперь определяем положением центра и радиусы окружностей, представляющих собой линии потока:

см

3.4. Вычисление ёмкости по картине поля и сравнение с теоретическим значением.

Теоретическое значение ёмкости на единицу длины в осевом направлении:

Определение ёмкости по картине поля:

, где n – число линий потока, m – число линий равного потенциала

Найдем сначала число линий потока:

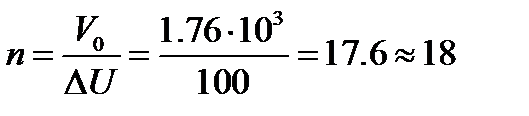
Тогда емкость равна:

Расхождение составляет:

3.5. Определение максимального gradU.

Градиент потенциала максимален на поверхности цилиндра меньшего радиуса и может быть вычислен как напряженность электрического поля с обратным знаком, создаваемая двумя заряженными противоположно по знаку нитями в точке с координатой :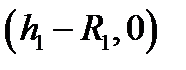

Максимальный gradU по картине поля:

Вблизи цилиндра :

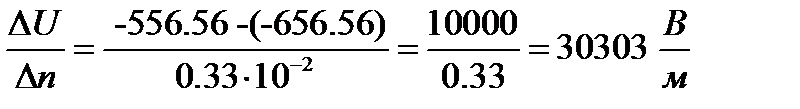
Расхождение составляет:

Дата добавления: 2015-08-17