Центральный ботанический сад им. Н.М. Гришко (Украина, г.Киев)

Место расположения сада настолько замечательное, что делает ботанический сад непохожим на все другие сады: 170 га прекрасного природного ландшафта почти в Центре города, выразительный рельеф, отличная визуальная и композиционная связь с р. Днепром, Левобережьем, мемориальным комплексом «Украинский государственный музей истории Великой Отечественной войны 1941—1945 годов», архитектурно-ландшафтным ансамблем Киево-Печерского государственного историческо-культурного заповедника, ансамблем памятников архитектуры Выдубицкого монастыря. Сад занимает возвышенное плато, изрезанное старыми глубокими балками со склонами разной крутизны, территория его очень живописна. Эрозионные процессы в нескольких местах восточного склона к р. Днепр образовали почти вертикальные обрывы. Здесь имеются два старых оползневых цирка, характерные для правого берега реки. Разница в отметках рельефа достигает 90 м. Кроме нагорной части, сюда относится часть залива р. Днепр с Выдубицким озером площадью около 30 га. Многие участки сада впечатляют целостностью, законченностью своей объемно-пространственной композиции, обоснованностью функционально-целевого и архитектурно-эстетического решения территории ботанического сада.

·

·

·

·

http://beautofan.ru | http://beholidays.ru | http://smipress.ru | http://realty10.ru

Образотворче мистецтво в 19 столітті

Тарас Шевченко. Селянська родина

І у 19 столітті головним центром освіти в Російській імперії залишилась Академія мистецтв у Петербурзі, проте багатьох художників приваблювала й Україна. Починається розвиток такого напряму як реалізм. Серед українських представників реалізму в образотворчому мистецтві Олекса Венеціанов, Іван Сошенко, Дмитро Безперчий. Визначною особистістю, творившою саме у той час став Тарас Шевченко, який працював у декількох галузях малярства: портретній, жанровій, пейзажній, релігійній. Тісно пов'язана з Україною булла й доля художника-мариніста Івана Айвазовського, котрий велику частину життя провів у рідній Феодосії і заповів цьому місту свою картинну галерею. Не менш визначною булла й творчість Архипа Куїнджі, який народився поблизу Маріуполя. Художник володів неймовірним даром писати краєвиди та гру світла на хмарах, деревах, скелях. Багато видатних художників-передвижників 19 століття родом з України: Олександр Литовченко, Микола Ярошенко, а Микола Ге. Видатним майстром побутового жанру був Микола Пимоненко, «Шукач сонця» - Володимира Орловського був одним із засновників нового українського реалістичного пейзажу. Найкращим українським портретистом кінця 19 — початку 20 століть вважають Олександра Мурашка.

Іван Айвазовський.Дев'ятий вал

Определение синуса, косинуса и тангенса для любого угла от 0° до 180°

До сих пор значения синуса, косинуса и тангенса были определены только для острых углов. Теперь мы определим их для любого угла от 0° до 180°.

Возьмем окружность на плоскости ху с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси X в верхнюю полуплоскость (полуплоскость, где y>0) угол а. Пусть х и у — координаты точки А. Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно:

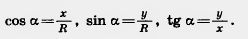
Определим теперь значения sin а, cos а и tg а этими формулами для любого угла а. (Для tg а угол а = 90° исключается.)

При таком определении sin 90° = 1, cos 90° = О, sin 180° = О, cos 180° = — 1, tg 180° = 0.

Считая, что совпадающие лучи образуют угол 0°, будем иметь: sinO° = 0, cosO° = l, tgO° = 0.

Докажем, что длм любого угла а, 0°<:а<:180°, sin (180° — а)=sin а, cos (180° — а) = — cos а. Для угла а ^ 90° tg (180° - а) = - tg а.

Действительно, треугольники ОАВ и ОА\В\ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников

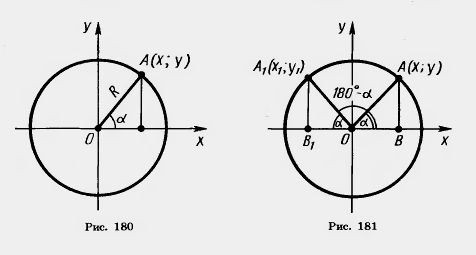
следует, что АВ=А₁В₁, т. е. у = у₁; ОВ=ОВ₁ следовательно, x= —x₁. Поэтому

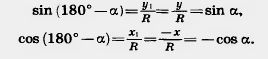
Разделив почленно равенство sin (180° —а) = sin а на равенство cos (180° — а)=—cos а, получаем:

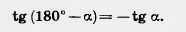
Что и требовалось доказать.

Здравствуйте! Тема урока – «Синус, косинус, тангенс угла. Основное тригонометрическое тождество». С понятием синус, косинус и тангенс угла мы уже встречались для острого угла прямоугольного треугольника. Здесь мы распространим эти понятия для любого угла из отрезка [0º;180º]. Теперь рассмотрим любой угол a Î [0º;180º]. Не будем связываться ни с каким прямоугольным треугольником, чтобы определить синус и косинус угла

Рисунок

Единичная полуокружность, оси координат. Угол a – это прежде всего вершина, вот она вершина. Два луча, один луч по оси х, а второй луч ОМ определяет этот угол a. Значит, луч пересекает полуокружность в единственной точке М. Точка М имеет две координаты – абсциссу, ординату (х_a; у_a).

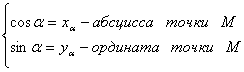
Абсциссу назвали косинусом угла, ординату назвали синусом угла. Итак, мы определили синус и косинус угла, не прибегая к помощи прямоугольного треугольника. Еще раз повторим: точка М единственная, определяется углом, у точки есть две координаты. Одну назвали косинусом вот этого угла, а вторую синусом этого же угла. Здесь нарисован угол все же острый, на следующем рисунке он будет тупым.

Рисунок

Пусть теперь угол b тупой. Определение синуса, косинуса вводятся аналогично. Единичная полуокружность, угол b тупой. Угол – это вершина, один луч фиксированный, второй луч ОN, который определяет угол b, дает точку N при пересечении с единичной полуокружностью. У точки N единственная пара координат (х_b; у_b) абсцисса и ордината. Абсциссу назвали косинусом угла b. Ординату назвали синусом угла b.

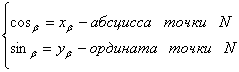
То есть определение то же самое. Мы продемонстрировали определение синуса и косинуса для тупого угла. Теперь мы готовы к строгим определениям синуса и косинуса произвольного угла из промежутка 0 a 180º.

Тот же рисунок.

Единичная полуокружность, угол a, луч ОМ высекает на этой окружности единственную точку М, она, и только она, задается этим углом. Точка М имеет две координаты, одну назвали 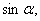другую 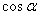. Итак, строгие определения. Для любого угла a из промежутка 0 a 180º синусом угла a называется ордината у точки М, а косинусом угла a абсцисса х точки М.

Итак, определения даны. В каких пределах могут меняться синус и косинус? Это наглядно видно. 0 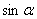1, -1 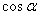1, это зафиксировано здесь.

Итак, определение синуса и косинуса для любого угла из заданного промежутка 0 a 180º нами сделано. Теперь рассмотрим конкретные примеры, которые – с одной стороны – решаются исходя из определения синуса и косинуса, и – с другой стороны – разъясняет нам эти определения.

Первый пример для угла в 0º, т.е. для координат точки A (1; 0).

1) А (1; 0) = А ( )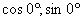

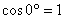
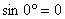
Второй пример для угла в 90º. 90º соответствующая точка С (0; 1) или С ( ).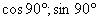

2) С(0;1) = С( 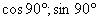). Значит, , .

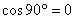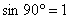И, наконец, для третьего угла, угла в 180º (ему соответствует точка В (- 1; 0) или В ( ).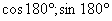

3) В (-1; 0) = В ( ).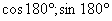

Теперь понятно, что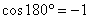

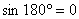
Итак, мы знаем, что такое синус угла, что такое косинус угла, умеем вычислять значения синуса и косинуса. Теперь с помощью этих понятий определим тангенс.

Тангенсом угла a (a ≠90º) называется отношение 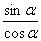, т.е. 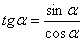при a= 90º 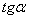не определен, поскольку косинус 90º=0, знаменатель равен 0, что невозможно.

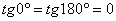, потому что синус здесь равен 0, а косинус не равен 0.

Теперь другое важное определение. Определение котангенса. Котангенсом угла a (a ≠0, a ≠180º) называется отношение 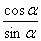, т.е. имеем формулу 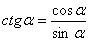. Пример: .

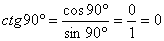А почему здесь (a ≠0, a ≠180º) такая оговорка? Потому что при этих углах синус равен 0, что невозможно. В знаменателе не должен стоять 0.

Отметим также формулу, связь котангенса и тангенса, 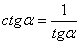. Итак, мы определили и тангенс a, и котангенс a, и связь между ними.

Каким образом найти синус и косинус какого-либо угла? Мы уже занимались этим. Вот есть угол. Первое, что мы находили, – это точку М. Затем находили координаты точки М, т.е. проектировали точку М на оси координат и соответствующим образом находили синус и косинус данного угла. Теперь все наши действия облечем в такое правило. Чтобы найти синус a и косинус a, надо, во-первых, провести луч ОМ, спроектировать соответствующую точку М полуокружности на оси координат. И тогда абсцисса точки М даст косинус угла, а ордината точки даст синус угла. Подчеркнем, что угол здесь лежит в пределах от 0 до 180º. Правило сформулировано.

Теперь рассмотрим основное тригонометрическое тождество. Вспомним, единичная полуокружность, угол a высекает точку М (х_a; у_a), назвали косинусом угла и синусом угла. Итак, единичная полуокружность. Основное тригонометрическое тождество вытекает из уравнения единичной окружности, вспомним его: это х²+у²=1. Уравнение единичной окружности с центром в начале координат.

Но х – это косинус угла, у – это синус угла, и в результате получаем основное тригонометрическое тождество: 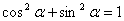. Подчеркнем, что a здесь любое a Î[0º;180º]. Ранее мы знали это тождество для углов a Î(0º; 90º). Таким образом, основное тригонометрическое тождество теперь для нас справедливо для всех углов a Î[0º;180º].

Теперь рассмотрим формулы приведения.

1)

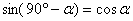
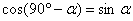при 0º a 90º. Это первая группа.

2)

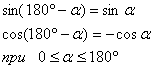
Строгое доказательство этих формул предстоит нам в курсе алгебры. А сейчас просто почувствуем, почему они справедливы. Рассмотрим формулы вторые. Вот угол a, вот соответствующая точка М, вот косинус, вот синус a. Вот угол (180º-a), соответствующая точка N, 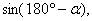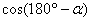. Заметим равенство треугольников ОММ₁ = ОNN₁. Почему они равны? По гипотенузе и острому углу, а значит, все их соответственные элементы равны друг другу. В частности, катет ММ₁ равен катету NN₁, а это есть не что иное, как синус одного и второго угла. Значит, синусы равны .

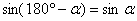Вторые катеты тоже равны: ОМ₁ = ОN₁ – значит, 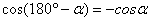. Таким образом, мы рассмотрели формулы приведения.

Итак, мы определили понятие синуса, косинуса, тангенса, котангенса угла для любого угла из отрезка [0º;180º]. Вывели основное тригонометрическое тождество. Далее синус и косинус будут использованы для определения координат точки.

Еще можно попробовать нарисовать деревья не привычной нам формы, а какие-нибудь необычные, замысловатые, сказочные. Например, такие.

Таким образом можно нарисовать целый осенний лес.

- при помощи обычного пульверизатора для цветов разбрызгать краску, смешанную с небольшим количеством воды. Если у вас нет пульверизатор, то его заменит старая зубная щетка или жесткая кисточка.

Дата добавления: 2015-08-17