Многогранники

Многогранник – это тело, граница которого состоит из кусков плоскостей (многоугольников). Эти многоугольники называются гранями, их стороны – рёбрами, их вершины – вершинами многогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналями многогранника. Многогранник – выпуклый, если все его диагонали расположены внутри него.

Развёртка поверхности, фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными.

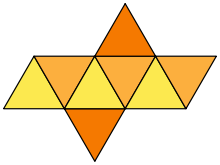
Развёртка октаэдра на плоскости

В технике развёрткой называют плоскую заготовку или чертёж плоской заготовки, из которой получают объёмную форму детали или конструкции путём изгибания. В этом случае развёртка не вполне отвечает математическому определению, из-за необходимости учёта изменения длин изгибаемого материала.

Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней.

Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство: В - Р + Г = 2, где В - число вершин, Р - число ребер и Г - число граней данного мно­гогранника.

Докажем, что для полученного разбиения многоугольника на более мелкие многоугольники имеет место равенство:

(*) В - Р + Г ' = 1,

где В – общее число вершин, Р – общее число ребер и Г ' – число многоугольников, входящих в разбиение. Ясно, что Г '= Г – 1, где Г – число граней данного мно­гогранника.

Действитель­но, после проведения диагонали в новом разбиении будет В вершин, Р+1 ребер и количество многоугольников увеличится на единицу. (рис. 5, а). Следовательно, имеем

В - (Р + 1) + (Г '+1) = В – Р + Г '.

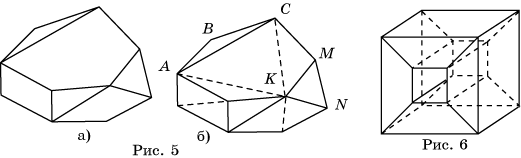
Пользуясь этим свойством, проведем диагонали, разбивающие входя­щие многоугольники на треугольники, и для полученного разбиения пока­жем выполнимость равенства (*) (рис.5, б). Для этого будем последо­вательно убирать внешние ребра, уменьшая количество треугольников. При этом возможны два случая:

а) для удаления треугольника ABC требуется снять два ребра, в на­шем случае AB и BC;

б) для удаления треугольника MKN требуется снять одно ребро, в нашем случае MN.

В обоих случаях равенство (*) не изменится. Например, в первом случае после удаления треугольника граф будет состоять из В – 1 вершин, Р – 2 ребер и Г ' – 1 многоугольника:

(В - 1) - (Р + 2) + (Г ' – 1) = В – Р + Г '.

Таким образом, удаление одного треугольника не меняет равенство (*). Продолжая этот процесс удаления треугольников, в конце концов, мы придем к разбиению, состоящему из одного треугольника. Для такого раз­биения В = 3, Р = 3, Г ' = 1 и, следовательно, B – Р + Г ' = 1. Значит, равенство (*) имеет место и для исходного разбиения, откуда оконча­тельно получаем, что для данного разбиения многоугольника справедливо равенство (*). Таким образом, для исходного выпуклого многогранника справедливо равенство В - Р + Г = 2.

Пример многогранника, для которого не выполняется соотношение Эйлера, показан на рисунке 6. Этот многогранник имеет 16 вершин, 32 ребра и 16 граней. Таким образом, для этого многогранника выполняется равенство В – Р + Г = 0.

Правильный многогранник или платоново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.

Многогранник называется правильным, если:

1. он выпуклый;

2. все его грани являются равными правильными многоугольниками;

3. в каждой его вершине сходится одинаковое число рёбер.

Дата добавления: 2015-08-17