ДЕ2.Аналитическая геометрия

Тема: Прямоугольные координаты на плоскости
Даны три вершины параллелограмма: , , 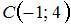.Тогда четвертая вершина 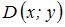, противолежащая вершине В, имеет координаты .

Решение:
Воспользуемся формулой деления отрезка пополам. Координаты точки 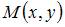, делящей отрезок между точками и 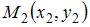пополам, находятся по формулам: 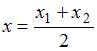, . Найдем координаты точки М пересечения диагоналей параллелограмма как координаты середины отрезка АС (диагонали параллелограмма точкой пересечения делятся пополам): , . Зная координаты точек В и М (как середины отрезка ВД) найдем координаты точки 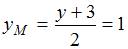то есть точка имеет координаты .

Тема: Прямая линия в пространстве
Острый угол между прямыми и равен

Решение:
Угол между прямыми определяется как угол между их направляющими векторами: и который можно вычислить по формуле:

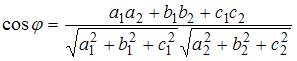тогда

Тема: Кривые второго порядка
Мнимая полуось гиперболы равна …

Тема: Плоскость в пространстве
Нормальное уравнение плоскости имеет вид …

Тема: Плоскость в пространстве
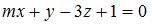Плоскости и перпендикулярны при значении , равном

Решение:
Плоскости, заданные общими уравнениями и перпендикулярны при условии, что . Тогда то есть .

Тема: Кривые второго порядка
Расстояние между фокусами гиперболы равно 10.

Тема: Прямая линия в пространстве
Параметрические уравнения прямой, параллельной оси 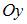и проходящей через точку имеют вид …

Решение:
Параметрические уравнения прямой, проходящей через точку с направляющим вектором имеют вид .За направляющий вектор прямой можно взять

Тогда или

Тема: Прямоугольные координаты на плоскости
Точка лежит на оси абсцисс и равноудалена от точки 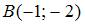и начала координат. Тогда точка имеет координаты …

Решение:
Так как точка лежит на оси абсцисс, то ее ордината . Так как точка равноудалена от точки 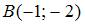и начала координат 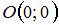, то расстояния от точки до точек 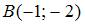и 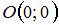равны. Тогда или

, т.е.

Тема: Плоскость в пространстве
Общее уравнение плоскости, проходящей через точку перпендикулярно прямой имеет вид …

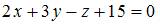
Решение:
Уравнение плоскости, проходящей через точку с нормальным вектором , имеет вид: .
Так как эта плоскость перпендикулярна прямой , то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть . Тогда
или .

Тема: Кривые второго порядка
Асимптоты гиперболы 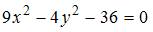задаются уравнениями …

Решение:
Асимптоты гиперболы задаются уравнениями вида . Разделив обе части уравнения 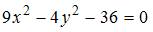на 36, получим каноническое уравнение гиперболы: . То есть и 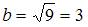. Тогда уравнения асимптот примут вид .

Тема: Прямая линия в пространстве
Расстояние между прямой и плоскостью равно …

Решение:
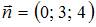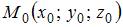Направляющий вектор прямой имеет вид , а нормальный вектор плоскости: . Скалярное произведение этих векторов равно нулю: . Следовательно, прямая либо параллельна плоскости, либо принадлежит ей. Тогда расстояние между прямой и плоскостью можно найти как расстояние между любой точкой данной прямой и плоскостью. В качестве такой точки возьмем, например, . Расстояние от точки до плоскости 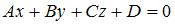найдем по формуле 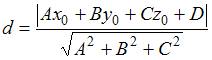, то есть

Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точки , и , имеет вид …

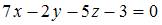
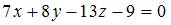
Решение:
Уравнение плоскости, проходящей через точки , и , не лежащие на одной прямой, имеет вид .
Подставим числовые значения в полученное уравнение: , или .
Раскрывая определитель по первой строке, получим ,
то есть

Тема: Прямоугольные координаты на плоскости
Точки и лежат на одной прямой, параллельной оси ординат. Расстояние между точками и 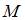равно 6. Тогда положительные координаты точки 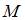равны …

,

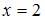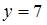
Тема: Прямая линия в пространстве
Параметрические уравнения прямой, параллельной оси и проходящей через точку имеют вид …

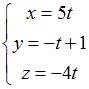
Решение:
Параметрические уравнения прямой, проходящей через точку с направляющим вектором , имеют вид .
За направляющий вектор прямой можно взять .
Тогда или

Тема: Прямоугольные координаты на плоскости
Точки , и лежат на одной прямой. Тогда точка делит отрезок в отношении …

Решение:
Делением отрезка в заданном отношении называется поиск такой точки на отрезке , которая удовлетворяет соотношению . Тогда искомый параметр будет равен:

Тема: Плоскость в пространстве
Общее уравнение плоскости, проходящей через точку параллельно плоскости , имеет вид …

Решение:
Уравнение плоскости, параллельной плоскости имеет вид: 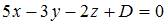. Подставим координаты точки в это уравнение: . Тогда .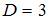

Тема: Кривые второго порядка
Мнимая полуось гиперболы равна … 3

Тема: Плоскость в пространстве
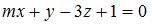Плоскости и перпендикулярны при значении , равном …

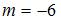
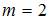
Тема: Прямая линия в пространстве
Прямая 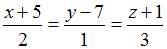параллельна плоскости , если параметр равен …

			– 11
			– 7

Решение:
Прямая параллельна плоскости, если скалярное произведение направляющего вектора прямой и нормального вектора плоскости равно нулю. То есть , или .

Тема: Прямоугольные координаты на плоскости
Даны три вершины параллелограмма: , , 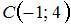. Тогда четвертая вершина 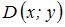, противолежащая вершине , имеет координаты …

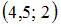
Тема: Кривые второго порядка
Соотношение 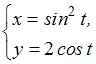в прямоугольной декартовой системе координат задает …

			параболу
			гиперболу
			эллипс
			окружность

Решение:
Вычислим 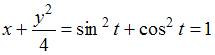, то есть .
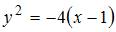Тогда в прямоугольной декартовой системе координат данное уравнение задает параболу с вершиной в точке

Тема: Прямоугольные координаты на плоскости
В треугольнике с вершинам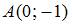и , и проведена медиана , длина которой равна …

Решение:
Точка 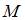является серединой отрезка . Координаты середины отрезка определяются по формулам , . Подставляя в эти формулы координаты точек и , получим координаты точки 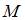: , . Расстояние между точками и 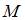можно найти по формуле .
То есть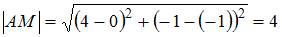

Тема: Плоскость в пространстве
Общее уравнение плоскости, проходящей через точку параллельно плоскости , имеет вид …

Решение:
Уравнение плоскости, параллельной плоскости имеет вид: 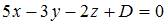. Подставим координаты точки в это уравнение: . Тогда .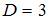

Тема: Кривые второго порядка
Фокусы эллипса имеют координаты и , а его эксцентриситет равен 0,6. Тогда каноническое уравнение эллипса имеет вид …

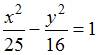
Решение:
Каноническое уравнение эллипса имеет вид ; фокусы эллипса имеют координаты и , где , а эксцентриситет .
Тогда , , .
Следовательно, получаем уравнение

Тема: Плоскость в пространстве
Общее уравнение плоскости, проходящей через точку перпендикулярно прямой , имеет вид …

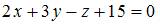
Решение:
Уравнение плоскости, проходящей через точку с нормальным вектором , имеет вид: .
Так как эта плоскость перпендикулярна прямой , то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть . Тогда
или .

Тема: Прямоугольные координаты на плоскости
Даны точк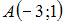и и . Тогда координаты точки 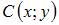, симметричной точке относительно точки , равны …

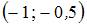
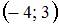
Тема: Прямая линия в пространстве
Параметрические уравнения прямой, параллельной оси и проходящей через точку имеют вид …

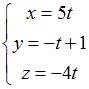
Решение:
Параметрические уравнения прямой, проходящей через точку с направляющим вектором , имеют вид .
За направляющий вектор прямой можно взять .
Тогда или .

Тема: Кривые второго порядка
Центр окружности 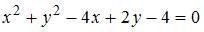имеет координаты …

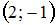
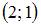
Решение:
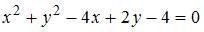Окружность радиуса с центром в точке задается на плоскости уравнением . Выделим в уравнении полные квадраты: , или .
Тогда центр окружности имеет координаты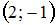

Тема: Кривые второго порядка
Вершина параболы имеет координаты …

Решение:
Выделим в уравнении полный квадрат: или . Тогда вершина параболы имеет координаты

o Математика (4)

o Информатика (2)

o Физика (2)

o Русский язык (0)

o Обществознание (0)

o История (0)

o Английский язык (2)

o Биология (0)

o География (0)

o Химия (0)

o Экономика (1)

o Решебники

o Презентации PowerPoint

o Расчетки

o Материалы

o Шпаргалки

o Лабораторные работы

o Разное

o Курсовые

o Дипломы

o Решение задач

o Видеоуроки

Дата добавления: 2015-08-17