Аналитическая геометрия

13. На плоскости 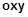заданы три точки 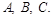Составить каноническое, общее и приведенное уравнения:

а) прямой 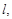проходящей через две точк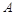и и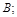

б) прямой 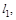проходящей через точку 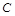параллельно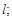

в) прямой 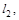проходящей через точку С перпендикулярно .

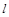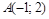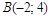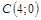
1)	;	;		2)	;	;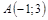
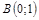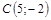
3)	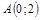;	;		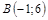4)	;	;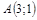
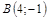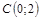
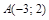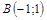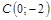
5)	;	;		6)	;	;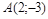
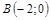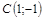
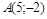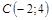
7)	;	;		8)	;	;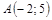
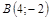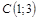
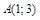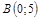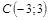
9)	;	;		10)	;	;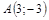
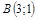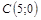
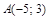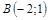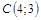
11)	;	;		12)	;	;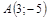
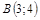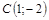
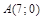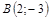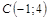
13)	;	;		14)	;	;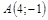
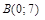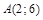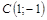
15)	;	;		16)	;	;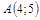

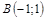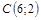
14. На плоскости 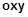даны две прямые и 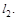Если они пересекаются, то найти координаты точки М их пересечения и угол между прямыми.

1)
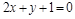
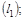
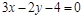
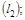
2)
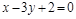
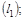
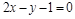
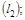
3)
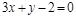
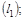
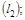
4)
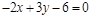
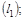
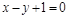
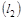
5)
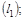
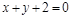
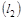
6)
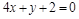
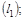
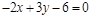
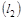
7)
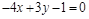
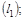
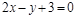
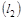
8)
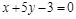
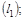
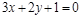
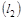
9)
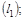
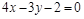
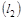
10)
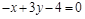
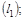
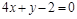
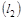
11)
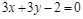
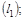
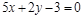
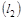
12)
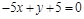
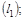
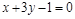
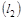
13)
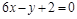
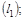
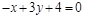
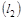
14)
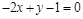
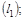
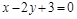
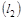
15)
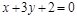
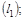
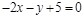
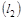
16)

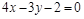
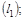
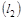
15. В пространстве даны четыре точки

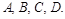
а) Составить уравнение плоскости 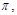содержащей три точки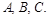

б) Составить уравнение плоскости 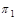проходящей через точку 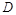параллельно плоскости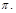

в) Найти расстояние между плоскостям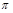и и

Варианты значений координат точек 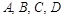взять из задач п. 8 и 10.

16. Даны две плоскост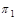и и 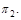Найти угол между ними.

1)
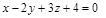
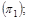
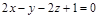
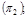
2)
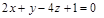
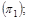
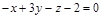
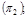
3)
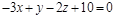
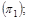
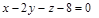
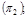
4)
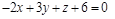
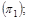
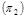
5)
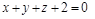
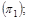
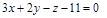
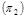
6)
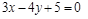
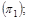
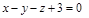
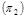
7)
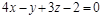
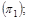
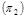
8)
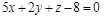
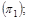
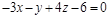
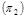
9)
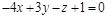
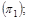
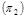
10)
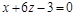
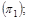
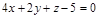
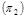
11)
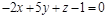
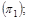
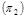
12)
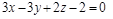
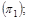
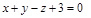
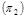
13)
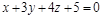
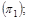
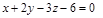
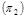
14)
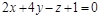
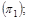
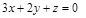
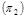
15)
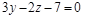
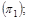
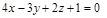
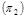
16)

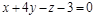
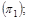
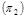
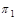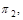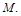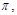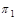17. Даны две плоскости и а также точка Составить уравнение плоскости проходящей через точку перпендикулярно обеим плоскостям и 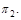Варианты уравнений плоскостей взять из п.16, а соответствующие им варианты значений координат точки М следующие:

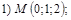
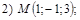
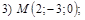
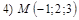
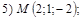
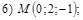
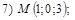
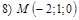
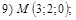
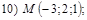
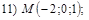
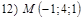
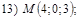
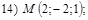
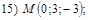
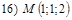
18. В пространстве составить канонические и общие уравнения прямой, проходящей через две заданные точки и .

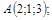
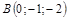
1)			2)
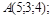
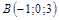
3)			4)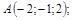
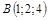
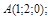
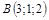
5)			6)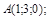
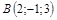
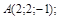
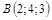
7)			8)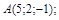
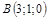
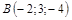
9)			10)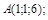
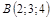
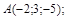
11)			12)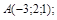
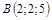
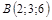
13)			14)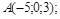
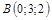
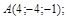
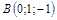
15)			16)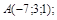

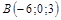
20. В пространстве своими каноническими уравнениями заданы две прямые и , а также задана точка .

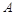а) Составить канонические уравнения прямой 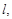проходящей через точку 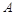перпендикулярно обеим прямым и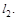

б) Составить уравнение плоскости 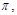проходящей через точку 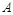параллельно обеим прямым и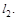

1)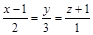
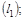
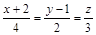
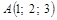
2)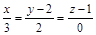
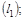
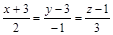
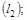
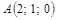
3)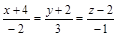
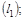
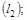
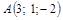
4)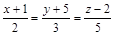
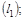
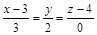
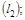
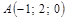
5)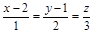
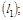
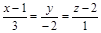
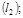
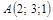
6)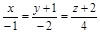
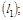
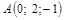
7)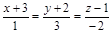
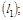
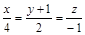
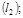
8)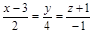
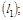
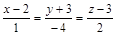
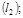
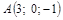
9)
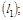
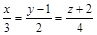
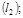
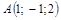
10)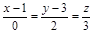
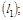
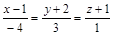
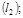
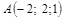
11)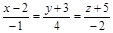
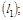
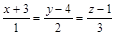
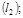
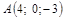
12)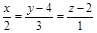
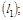
13)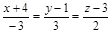
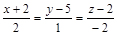
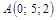
14)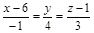
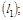
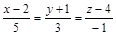
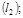
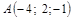
15)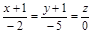
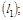
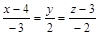
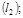
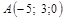
16)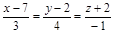

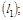
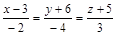
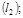
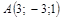
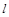21. В пространстве задана прямая и плоскость 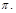Найти угол между ними и координаты точки их пересечения. Для каждого варианта в качестве уравнения прямой 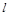взять уравнение прямой из п. 20, а в качестве уравнения плоскости 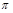взять уравнение плоскости 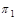из п. 16.

22. Задана плоскость 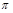и точка 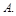Найти координаты проекци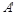и точки 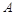на плоскость 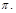Для каждого варианта в качестве уравнения плоскости 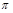взять уравнение плоскости из п. 16; значения координат точки 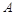взять из задач п.20.

Дата добавления: 2015-08-17