
Читайте также:
|
Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство
∆у≈dy, причем это равенство тем точнее, чем меньше ∆х.
7) Производная обратной функции
Дифференцируемая монотонная функция f: ] a, b [ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f -1, производная которой вычисляется по формуле
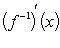
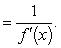
Дата добавления: 2015-08-17; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Касательная и нормаль к плоской кривой. | | | Производная параметрически заданной функции |