Касательная и нормаль к плоской кривой.

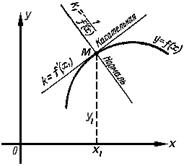
Пусть даны кривая y = f(x) и точка M (x₁; y₁) на ней. Требуется составить уравнения касательной и нормали (смотри рисунок).
Как известно, угловой коэффициент k касательной к кривой y = f(x) в точке M (x₁; y₁) равен значению f '(x₁) производной y' = f '(x) при x = x₁ / Следовательно, уравнение касательной можно записать в виде уравнения прямой, проходящей через данную точку в данном направлении, т.е. в виде

y - y₁ = f '(x₁)(x - x₁)

Нормалью называется прямая, проходящая через точку касания перпендикулярно касательной. поэтому ее угловой коэффициент равен 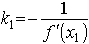, а уравнение записывается в виде

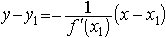
6) Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х. В этом и состоит геометрический смысл дифференциала.

Дата добавления: 2015-08-17