Модели реакторов с неидеальной структурой потоков

Математическая модель реактора с неидеальной структурой потоков должна удовлетворять ряду требований:

1) она должна точнее, чем модели реакторов с идеальной структурой потока, передавать закономерности протекающего химического процесса, в частности, при моделировании проточных реакторов расчет на основе такой модели должен позволить получить распределение концентраций по объему, приближающееся к реальному;

2) модель при большей сложности (по сравнению с моделями идеальных реакторов) должна быть такой, чтобы при ее использовании можно было аналитическими или численными методами получить расчетные зависимости, необходимые для определения размеров реактора или решения подобных задач.

3) дополнительное требование: при некоторых предельных значениях коэффициентов, входящих в уравнения модели, она должна описывать либо проточный реактор идеального смешения, либо — идеального вытеснения.

При разработке тех или иных моделей следует иметь в виду, что, как правило, теория дает общий вид уравнений математического описания, а числовые коэффициенты этих уравнений, значения которых отличают один частный случай от другого, должны быть найдены экспериментально. Эти коэффициенты называют параметрами математической модели. Обычно стремятся к тому, чтобы число таких параметров было минимальным. Большое число параметров, с одной стороны, вроде бы делает модель точной (физически), но, однако, при этом возникает опасность появления значительных ошибок, так как чем больше параметров, тем более точный эксперимент нужно поставить, чтобы достаточно верно оценить их. Математические модели неидеальных реакторов могут быть построены на основе двух подходов. Первый основан на мысленной замене реального реактора той или иной комбинацией идеальных аппаратов. Второй подход имеет большее физическое обоснование - при составлении математического описания процесса стремятся учесть те реальные физическое явления, происходящие в аппарате, и внести их в уравнения модели с помощью соответствующих математических операторов.

Очевидно, что при первом подходе математическая модель будет представлять собой систему уравнений, объединяющих математические описания нескольких идеальных реакторов. Число уравнений может быть велико, но по структуре они останутся такими, же простыми, как и уравнения идеальных моделей. При втором подходе число уравнений может быть меньше, но уравнения более сложные, а следовательно, сложнее и методы их решения.

Наиболее распространенными являются две однопараметрические модели: ячеечная и диффузионная.

Ячеечная модель. В ячеечной модели использован первый подход к описанию реальных реакторов, а именно: реальный аппарат мысленно расчленяют на N последовательно соединенных ячеек идеального смешения. Суммарный объем всех ячеек равен полному объему реактора. Правомерность такой замены вытекает из сравнения каскада реакторов идеального смешения.

Ячеечная модель (модель каскада реакторов идеального смешения) представляет собой, как известно, систему из N уравнений материального баланса по компоненту J (при описании простой реакции), каждое из которых имеет вид

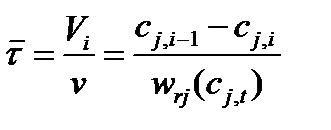(39)

При N = 1 уравнение (39) описывает, естественно, единичный реактор идеального смешения

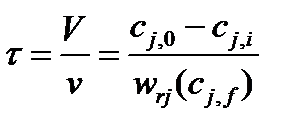(21)

При N 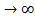и бесконечно малых объемах секций V_i суммарное время пребывания в каскаде из N реакторов можно рассматривать как некоторый предел суммы

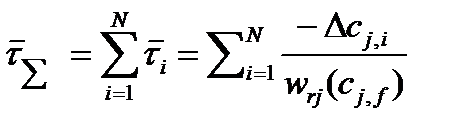(40)

Где 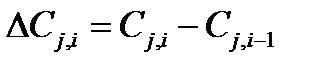.Очевидно, что этот предел можно рассматривать как интеграл

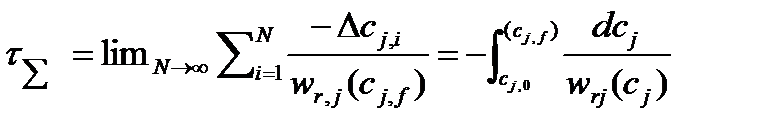(41)

Сравнивая уравнения (41) и (14), можно сделать вывод, что при N 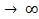ячеечная модель (модель каскада реакторов идеального смешения) вырождается в модель проточного реактора идеального вытеснения.

Таким образом, с помощью модели каскада реакторов идеального смешения можно описать предельные гидродинамические режимы. Разумно предположить, что и промежуточный режим (а в любом реальном реакторе гидродинамическая обстановка отвечает именно промежуточному режиму) можно описать с помощью модели каскада реакторов идеального смешения, состоящего из N ячеек, причем, с одной стороны, N 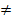1, а с другой — N является конечным числом. Как правило, применение ячеечной модели при N < 10 позволяет удовлетворительно описать реальный реактор.

Число ячеек N, заменяющих реальный реактор, и является единственным параметром ячеечной модели. При известном N расчет реактора на основе ячеечной модели по сути дела ничем не отличается от расчета каскада проточных реакторов идеального смешения и представляет собой последовательное решение уравнений математической модели каждой ячейки (секции) идеального смешения.

Однопараметрическая диффузионная модель. Диффузионная модель, как и ячеечная, описывает реальную гидродинамическую обстановку в проточном реакторе как некоторый промежуточный случай между режимами идеального смешения и идеального вытеснения. При построении диффузионной модели в отличие от модели идеального смешения учитывается неравномерность распределения параметров процесса (в частности, концентрации) по объему аппарата. Но неравномерным является и распределе­ние концентрации по длине реактора идеального вытеснения. В отличие от модели идеального вытеснения в диффузионной модели учитывается наличие перемешивания реакционной среды в осевом направлении, вызванное различными видами диффузии. Последнее условие и легло в основу названия модели—диффузионная.

В реальном реакторе неравномерное распределение концентраций и вызванный им диффузионный перенос имеют место как в продольном ( осевом), так и в радиальном направлениях. Однако учет и продольной, и радиальной диффузии чрезмерно усложнит уравнения диффузионной модели. Поэтому в первом приближении считают, что в ради-альном направлении распределение концентраций равномерное, и дифузия происходит только вдоль оси реактора.

Перенос вещества за счет турбулентной или тейлоровской диффузии может быть описан уравнениями, аналогичными уравнению для молекулярной диффузии, но со своими коэффициентами D_{Ty p6} и D_Teйл.,. Экспериментально разделить различные виды диффузии в реакторе невозможно. Поэтому целесообразно все их объединить одним уравнением с коэффициентом продольной диффузии D_L, который нельзя предсказать заранее теоретически в силу сложной природы этой величины. Коэффициент продольной диффузии D_L и является единственным параметром однопараметрической диффузионной модели.

В случае учета радиальной диффузии путем введения соответствующих операторов с коэффициентом радиальной диффузии Dr реактор будет описываться двухпараметрической диффузионной моделью.

Можно получить уравнение однопараметрической диффузии модели, взяв за основу уравнение материального баланса для элементарного объема проточного реактора (10) и упростив его в соответствии со следующими допущениями:

1) как и в модели идеального вытеснения, по сечению реактора, перпендикулярному основному потоку, все условия выровнены, т. е. концентрация, температура меняются только вдоль оси реактора;

2) в аппарате отсутствуют застойные зоны и байпасные потоки.

Как и для реактора идеального вытеснения, конвективный перенос вещества J будет происходить только в направлении оси z. От оператора диффузионного переноса D 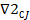также останется только составляющая вдоль оси г. Следовательно, уравнение (10) в применении к однопараметрической диффузионной модели примет вид:

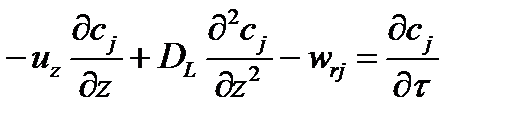(42)

где u_z = v/F - линейная скорость потока в направлении оси реактора.

Уравнение (42) описывает нестационарный процесс в реальном реакторе с распределенными параметрами при наличии перемешивания. Гидродинамическая обстановка в аппарате учитывается в этом уравнении двумя первыми членами. Первый член уравнения 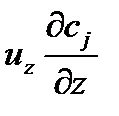характеризует конвективный перенос вещества J с линейной скоростью и_z. В результате протекания химической реакции по длине аппарата устанавливается распределение концентрации данного вещества, описываемое в точке с координатой z производной dc_j/dz. Второй член уравнения 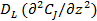описывает осевое перемешивание, интенсивность которого определяется коэффициентом продольной диффузии D_L.

В предельных случаях уравнение (42) может быть использовано для описания, как реактора идеального вытеснения, так и аппарата идеального смешения.

Действительно, если считать, что выполняется допущение о полном отсутствии осевого перемешивания, то .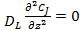

и уравнение (42) принимает такой же вид, как уравнение (24) для реактора идеального вытеснения:

.

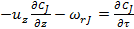Если же принять допущения о полном выравнивании концентрации по объему и дискретном скачкообразном изменении концентрации реагента 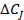на входе в проточный реактор, то в уравнении (42) можно будет пренебречь диффузионным оператором 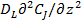(отсутствует причина для возникновения диффузионных потоков внутри аппарата), а производную 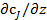в первом члене уравнения заменить на отношение конечных разностей, как это было сделано для проточного реактора идеального смешения. Тогда уравнение (42) будет совпадать с уравнением (21) для проточного реактора идеального смешения, т. е. можно сделать вывод, что сформулированное выше требование о необходимости предельного перехода неидеальных моделей в модели идеального вытеснения или смешения выполняется и для однопараметрической диффузионной модели.

Степень приближения реальной гидродинамической обстановки к одному из идеальных режимов зависит от степени взаимного влияния конвективной и диффузионной составляющей в уравнении материального баланса (42). Используя методы теории подобия, можно из дифференциального уравнения (42) получить критерий подобия, являющийся мерой относительной эффективности двух физических процессов: конвективного переноса в направлении оси реактора и продольного диффузионного перемешивания:

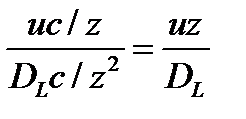(43)

где и — линейная скорость; z — линейный размер (удобнее его обозначить через L).

Полученный критерий называют диффузионным критерием Пекле

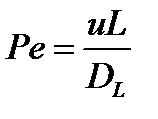(44)

иногда его называют также критерием Боденштейна (Во).

При больших значениях Ре интенсивность конвективного переноса существенно выше интенсивности продольного диффузионного перемешивания. Это имеет место в длинном канале (большие значения L) при высокой линейной скорости или низких значениях коэффициентапродольной диффузии D _L. При Ре 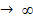реактор вырождается в аппаратидеального вытеснения.

При малых числовых значениях Ре (короткий канал, невысокие линейныескорости или большие значения D_L) относительная интенсивность продольного перемешивания превышает интенсивность продольного конвективного переноса. При Ре 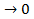реактор вырождается в аппарат идеального смешения: бесконечно быстрая диффузия приводит к полному и мгновенному выравниванию концентраций.

Дата добавления: 2015-08-20