Каскад реакторов идеального смешения

Каскад представляет собой несколько последовательно соединенных проточных реакторов (секций) идеального смешения (рис. 6). Реакционная смесь последовательно проходит через все секции. Можно рассматривать в качестве примера такой модели не только систему последовательно расположенных отдельных аппаратов, но и проточный реактор, тем или иным образом разделенный внутри на секции, в каж-

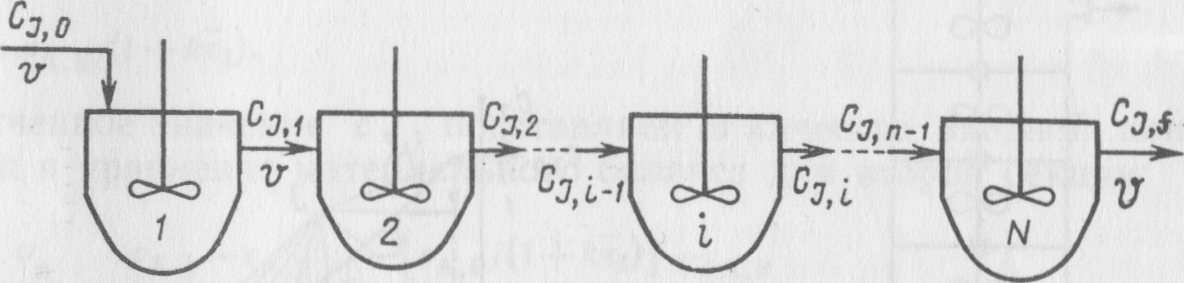
Рис. 6.Каскад реакторов идеального смешения

дой из которых осуществляется перемешивание реакционной смеси (рис.7). Например, близка к такому типу аппарата тарельчатая барботажная колонна.

Для каскада реакторов идеального смешения должны выполняться следующие допущения об идеальности:

1)в каждой секции каскада выполняются условия реактора идеального смешения, т. е. мгновенное изменение параметров процесса, равенство параметров во всех точках секции и в потоке, выходящем из нее;

2) отсутствие обратного влияния: каждый последующий реактор не влияет на предыдущий.

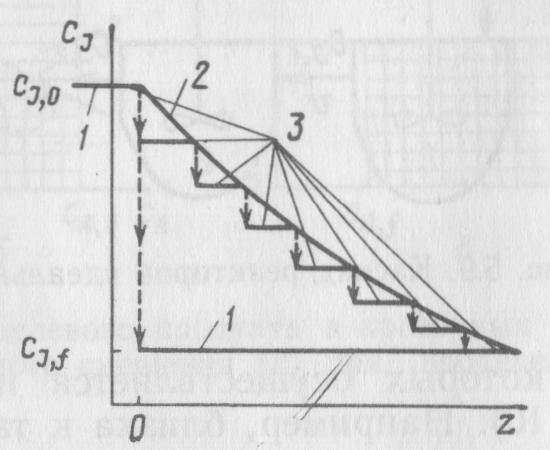
На рис. 8 сравнивается характер изменения концентрации исходного реагента при прохождении реакционной смеси через последовательные секции идеального смешения и через единичные реакторы идеального вытеснения и идеального смешения.

Математическая модель каскада реакторов идеального смешения, работающего в изотермическом режиме, представляет собой систему уравнений материального баланса по какому-либо участнику реакции, включающую, по меньшей мере, N уравнений по числу секций каскада. Уравнения материального баланса для любой из секций каскада однотипны. Материальный баланс по компоненту J для i -й секции в стационарном режиме работы каскада имеет вид

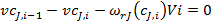(29)

Или 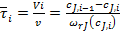, (30)

где Vi — реакционный объем i-й секции;

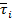— среднее время пребывания реакционной смеси в i -й секции;

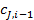— концентрация участии ка реакции J на входе в i-ю секцию, равная концентрации на выходе из (i — 1)-й секции;

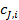— концентрация компонента J на выходе из i -й секциий.

Расчет каскада реакторов идеального смешения обычно сводится к определению числа секций заданного объема, необходимых для достижения определенной глубины превращения, или к определению состава реакционной смеси на выходе из i-й секции каскада.

Допущение об отсутствии обратного влияния в каскаде реакторов идеального смешения существенно упрощает расчет. По сути дела он сводится к последовательному решению уравнений материального баланса для каждой секции относительно концентрации реагента (или продукта) на выходе. Выходной параметр для первой секции (концентрация 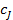),полученный из первого уравнения, является входным параметром для второй секции, выходной параметр второй секции — входным для третьей и т. д.

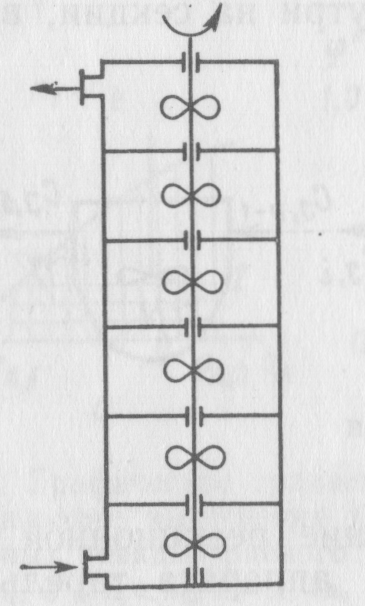
Рис. 7. Секционный аппарат с перемешиванием

Рнс. 8. Изменение концентрации реагента в единичном реакторе идеального смешения (1), реакторе идеального вытеснения (2) и каскаде реакторов идеального сме­шения (3)

Различают аналитический и численные методы расчета каскада. Применение аналитического метода возможно в том случае, если уравнения материального баланса могут быть аналитически решены относительно концентрации 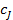. Это можно сделать, например, если протекающие реакции описываются кинетическими уравнениями первого или второго порядка.

Рассмотрим определение концентрации реагента А на выходе из каскада реакторов, включающего N секций равного объема 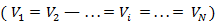при проведении реакции первого поряд­ка, скорость которой описывается уравнением = kc_A. Из уравне­ния материального баланса для первой секции

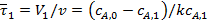(31)

Определяем 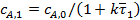(32)

Полученное значение 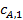подставляем в качестве входной концент­рации в уравнение материального баланса для второй секции:

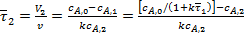(33)

из него определяем 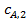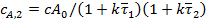. (34)

При равенстве объемов секций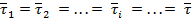

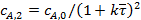. (35)

Продолжая аналогичные расчеты, для N - й(последней) секции каскада получим:

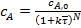. (36)

Если учесть, что 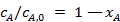, уравнение (36) можно записать в виде:

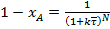, (37)

И тогда можно рассчитать число секций заданного объема, необходимых для достижения степени превращения :

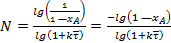. (38)

Если полученное при расчете по уравнению (38) N является дробным числом, его округляют в большую сторону для того, чтобы было выполнено условие 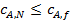Полученное уравнение (38) справедливо, естественно, только для реакции первого порядка.

Для реакций, описываемых кинетическими уравнениями, не позволяющими аналитически решить уравнение (29) относительно 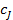(например, реакции дробного порядка), при расчете каскада приходится прибегать к численным методам. Так как уравнения материального баланса для всех секций однотипны, можно составить алгоритм решения этих уравнений для i -й секции и последовательно применить его N раз.

---

Дата добавления: 2015-08-20