Стивен Хокинг. Роджер беспокоится относительно бедного кота Шредингера

Роджер беспокоится относительно бедного кота Шредингера. Такой мысленный эксперимент вряд ли является политкорректным в настоящий момент. Роджер озабочен тем, что матрица плотности, учитывая состояния

|кот жив> и |кот мертв>,

с равными вероятностями, дает также равные вероятности для состояний

(|кот жив> + |кот мертв>) и (|кот жив> — |кот мертв>).

Так почему же мы наблюдаем либо |кот жив>, либо |кот мертв>? Почему мы не наблюдаем

или (|кот жив>+ |кот мертв>), или (|кот жив> — |кот мертв>)?

Первое, что я хотел бы сказать, что такая неоднозначность в собственных состояниях матрицы плотности может появиться лишь тогда, когда собственные значения точно совпадают. Если бы вероятности для |живой> и |мертвый> были слегка различны, неоднозначности в собственных состояниях не было бы. Эти базисы различаются по своим собственным векторам в матрице плотности. Так почему природа выбрала матрицу плотности диагональной в базисе |живой>/|мертвый>, а не в базисе |живой> + |мертвый>/|живой> — |мертвый>? Ответ состоит в том, что состояния |кот жив> и |кот мертв> на макроскопическом уровне отличаются такими вещами, как положением пули или раной кота. Когда мы отслеживаем все такие причины, которые мы не наблюдаем, как, например, возмущения плотности воздуха, то матричный элемент любой наблюдаемой между состояниями |кот жив> и |кот мертв> будет усредняться и давать нуль. Именно поэтому при наблюдениях мы всегда получаем, что |кот жив> или |кот мертв>, но никогда не получаем их комбинацию. Это обычная квантовая механика. При этом нет необходимости в новой теории измерений, а уж тем более в квантовой теории гравитации.

150 · Глава 7 — Стивен Хокинг и Роджер Пенроуз

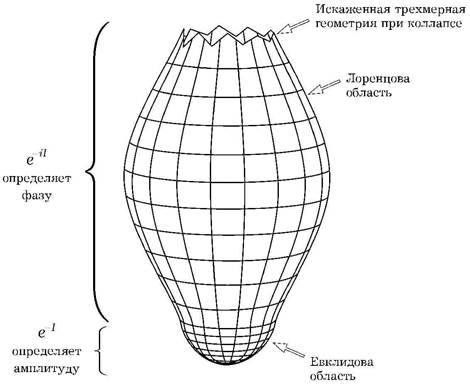
Вернемся к квантовой гравитации. Роджер, по-видимому, согласен с тем, что предложение об отсутствии границ может объяснить малость вейлевского тензора в ранней Вселенной. Однако он спрашивает, может ли она привести к большому значению тензора Вейля, которое, как ожидается, должно проявляться при гравитационном коллапсе черных дыр или коллапсе целой Вселенной. Я думаю, что это опять основано на неверном понимании ПОГ. Роджер, видимо, согласен с тем, что существуют лоренцевские решения, которые начинаются в ранней Вселенной и являются достаточно гладкими, а затем развиваются в сильно нерегулярную метрику при гравитационном коллапсе. Для ранней Вселенной можно соединить эти лоренцевские метрики с половиной евклидовой 4-сферы. Это приближенно дает метрику седловой точки для волновой функции в случае сильно искаженной 3-геометрии при коллапсе (рис. 7.4). Конечно, как я сказал раньше, точная метрика в седловой точке будет сложной и не будет ни лоренцевой, ни евклидовой. Тем не менее, в хорошем приближении ее можно разделить на области, которые будут близки к евклидовым или лоренцевским. Евклидова область будет только слегка отличаться от половины круглой 4-сферы. Тогда ее действие будет лишь чуть больше, чем для половины круглой 4-сферы, которая соответствует однородной и изотропной Вселенной. Лоренцевская часть решения будет сильно отличаться от такого однородного и изотропного решения. Однако действие этой лоренцевской части сказывается лишь на изменении фазы волновой функции и никак на амплитуде. Она определяется действием евклидовой части и почти не зависит от того, как возмущена 3-геометрия. Поэтому все 3-геометрии при гравитационном коллапсе равновероятны, что соответствует сильно нерегулярной метрике с большим значением кривизны Вейля. Я надеюсь, что это убедит Роджера и всех остальных в том, что предположение об отсутствии границ может объяснить, и почему ранняя Вселенная была гладкой, и почему гравитационный коллапс будет нерегулярным.

Последнее, на чем я хочу остановиться — это мысленный эксперимент с черной дырой в ящике. Роджер до сих пор убежден в том, что происходит уменьшение объема фазово-

Обсуждение · 151

Рис. 7.4. В процессе туннелирования к коллапсирующей 3-геометрии евклидово сечение определяет амплитуду волновой функции для 3-геометрии, в то время как лоренцевское сечение — ее фазу

го пространства, потому что многие различные конфигурации коллапсируют, образуя одну и ту же черную дыру. Но точка зрения термодинамики черных дыр состоит в том, что такое уменьшение фазового пространства не должно происходить. Возможность приписать черной дыре энтропию определяется тем, что дыра может быть образована e ^sспособами. При испарении симметричным во времени образом она излучает также e ^sспособами. Поэтому уменьшение объема фазового пространства отсутствует, и нет необходимости использовать для его компенсации R -процесс. Иначе говоря, я убежден в гравитационном коллапсе, но не в коллапсе волновой функции.

И, наконец, относительно моего заявления об одинаковости черных и белых дыр. Роджер возражает, что диаграммы Картера-Пенроуза для них очень различны (рис. 7.5). Я согласен, что они различны, но можно сказать, что это только

152 · Глава 7 — Стивен Хокинг и Роджер Пенроуз

Рис. 7.5. Диаграммы Картера-Пенроуза для черной и белой дыр

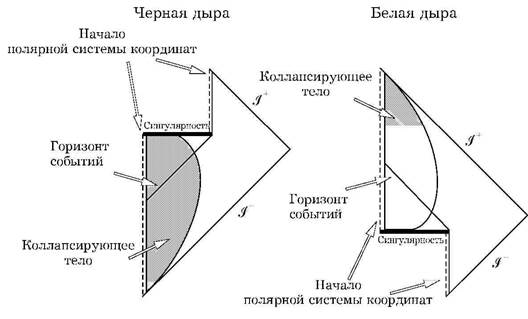
классическая картина. В квантовой теории я могу заявить, что черная и белая дыры являются одинаковыми объектами для внешнего наблюдателя. Но в ответ Роджер может спросить, а что же увидит тот человек, который падает в дыру? Увидит ли он или она диаграмму Картера-Пенроуза для черной дыры? Я думаю, что этот аргумент несостоятелен, так как он основан на предположении, что существует единственная метрика для пространства-времени, как в классической теории. В квантовой теории, в противоположность классической, мы должны вычислять интегралы по путям по всем возможным метрикам. В различных случаях при этом возникнут метрики в различных седловых точках. В частности, метрики в седловых точках для случая, когда вопросы задает внешний наблюдатель, будут отличаться от метрик в седловых точках для падающего наблюдателя. Можно себе также представить, что черная дыра излучает наблюдателя. Вероятность этого мала, но отлична от нуля. По-видимому, метрика седловой точки такого наблюдателя будет соответствовать диаграмме Картера-Пенроуза для белой дыры, поэтому мое утверждение о том, что черная и белая дыры по сути являются одним и тем же, самосогласованно. Это единственный естественный способ сделать квантовую гравитацию СРТ-инвариантной.

Обсуждение · 153

Дата добавления: 2015-08-20