Корреляционная зависимость и методы ее выявления.

В зависимостях одни признаки (факторные) выступают в качестве причин, обусловливающих изменение других признаков (результативных).

Вообще зависимости между признаками бывают либо функциональными (полное соответствие между изменениями факторного признака и изменениями результативной величины), либо корреляционными (нет полного соответствия, и воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении факторных данных).

Корреляционная связь – это такая связь, которая проявляется не в каждом отдельном случае, а в массе случаев в средних величинах в форме тенденции.

Статистическое исследование такой связи ставит своей конечной целью получение модели корреляционной зависимости для ее практического использования.

Основной задачей корреляционного метода является определение по данным большого числа наблюдений того, как с изменением факторного признака при прочих равных условиях меняется среднее значение результативного признака. Эта задача решается путем определения формы связи и нахождения уравнения этой связи двух или нескольких переменных.

Такая работа осуществляется в несколько этапов: 1. проводится логический анализ сущности изучаемого явления и причинно-следственных связей. В результате устанавливаются результативный показатель (у) и факторы его изменения (х₁, х₂, …, х_n). Связь только двух признаков у и х называется парной корреляцией. Корреляция бывает множественной, если на результативный признак влияют несколько факторов. При этом по общему направлению связи бывают прямыми (с увеличением признака х увеличивается и признак у) и обратными (наоборот); 2. устанавливается сам факт наличия и направления корреляционной зависимости (КЗ) между результативным и факторным признаками. Для выявления КС либо строят таблицу: сверху вниз по нарастающей – значения фактора, слева направо по нарастающей – значения результативного признака; тогда если частоты повторения данного сочетания факторного и результативного признаков концентрируются от сверху слева до вниз направо корреляция предполагается. Либо по методу аналитической группировки и определения групповых средних все единицы совокупности разбиваются на группы по величине факторного признака и для каждой группы определяется средняя величина результативного признака; по этим данным стоится график эмпирической линии связи (линии регрессии), вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о ее форме. 3. измеряется степень тесноты и проводится оценка существенности КС. Для определения степени тесноты парной линейной зависимости служит линейной коэффициент корреляции:

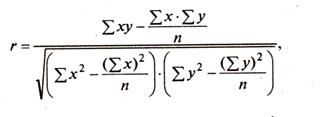
Чем ближе значение линейного коэффициента К (изменяется от «-» до «+» 1) по абсолютной величине к единице, тем связь теснее. Знак при нем указывает направление связи: «+» - соответствует прямой зависимости, а «-» - обратной. 4. после установления достаточной степени тесноты связи выполняется построение модели связи (уравнения регрессии).

Дата добавления: 2015-08-20