Основные теоретические положения

Прежде чем приступить к решению практических задач, необходимо понять сущность средней величины, являющейся обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Необходимо учесть, что средняя величина должна вычисляться с учетом экономического содержания определяемого показателя. Каждый показатель имеет свое, только ему присущее содержание. Такой подход позволяет правильно определить среднюю величину признака, выбрать форму средней.

Отдельные значения признака называются вариантами и обозначаются через х, число единиц в совокупности через п, объем совокупности – М, частота признака – f, средняя величина - .

Средняя арифметическая простая равна сумме отдельных значений признака, деленной на число этих значений. Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не повторяются. Простая средняя арифметическая определяется по формуле:

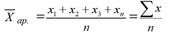
Если значения признака повторяются, то используется средняя арифметическая взвешенная. Она определяется по формуле:

В тех случаях, когда в совокупности нет количественного признака, но имеется общая величина совокупности, то используется средняя гармоническая. Она определяется по формуле:

Когда вместо индивидуальных значений признака представлены квадраты исходных величин, то применяют среднюю квадратическую. Она определяется по формуле:

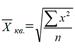
В статистике применяется структурная средняя: мода и медиана. Мода – значение признака, чаще всего встречающаяся в данной совокупности. В интервальном ряду распределения мода будет равна:

, где

Мо – мода,

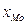-нижняя граница модального интервала,

- величина модального интервала,

- частота модального интервала,

- частота интервала, предшествующего модальному,

- частота интервала, последующего за модальным.

Медиана – величина признака, находящаяся в середине ряда. В четном ряду медиану определяют через накопление частоты. Для определения медианы необходимо сначала определить медианный интервал, которому соответствует накопленная частота, превышающая полусумму частот ряда.

, где

Ме – медиана,

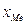-нижняя граница медианного интервала,

- величина медианного интервала,

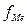- частота медианного интервала,

- полусумма частот ряда,

- накопленная частота, предшествующая медианному интервалу.

Величина признаков варьируют под действием различных причин и условий. Чем разнороднее условия, тем больше его вариация. Величина вариации признака в совокупности характеризует ее однородность. Основные показатели, характеризующие вариацию: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации (R) – простейший показатель, разность между максимальным (хmaх) и минимальным (хmin) значениями признака.

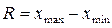
Среднее линейное отклонение взвешенное:

Дисперсия взвешенная:

Среднее квадратическое отклонение взвешенное:

Коэффициент вариации:

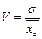
Коэффициент вариации(V) - это отношение среднеквадратического отклонения к средней величине признака.

Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценить её в единицах измерения исследуемой совокупности.

В отличие от них коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня.

Если коэффициент вариации не превышает 33%, то совокупность можно считать однородной.

Задачи

Задача 3.1. Рабочие бригады имеют следующий стаж работы на данном предприятии:

Табельный номер рабочего
Стаж работы, лет

Определите средний стаж работы.

Задача 3.2. Имеются данные о времени простоя станков по цехам завода:

Номер цеха	Время простоя станка за смену, мин.	Число станков

Определите среднее время простоя одного станка.

Задача 3.3. Имеются данные о заработной плате рабочих завода:

Номер цеха	Базисный период	Отчетный период
Средняя з/пл. одного рабочего, руб.	Численность рабочих, чел.	Средняя з/пл. одного рабочего, руб.	Фонд з/пл., тыс.руб.
				1646,2 2460,8 2058,6 6248,2

Определите среднюю заработную плату рабочего в целом по заводу:

1) в базисном периоде;

2) в отчетном периоде.

Сравните полученные данные. Укажите, какие виды средних необходимо применить в каждом случае.

Задача 3.4. Данные по предприятиям объединения, выпускающим однородную продукцию, за два периода:

Предприятие	Базисный период	Отчетный период
Затраты времени на единицу продукции, ч.	Произвдено продукции, тыс. шт.	Затраты времени на единицу продукции, ч.	Затраты времени на всю продукцию, тыс. ч..
1-е 2-е 3-е

Определите затраты времени на производство в среднем по объединению за каждый период. Обоснуйте применение формул средних для расчета заданных показателей.

Задача 3.5. Имеются данные о распределении банков по величине полученной прибыли за год:

Размер прибыли, млн.руб	Число банков
3,7-4,6 4,6-5,5 5,5-6,4 6,4-7,3 7,3-8,1

Определите:

1) средний размер прибыли одного банка;

2) моду;

3) медиану.

Задача 3.6. Себестоимость единицы одноименной продукции по предприятиям отрасли характеризуют следующие показатели:

Группы предприятий по себестоимости единицы продукции, тыс. руб.	Число предприятий
16-20 20-24 24-28 28-32 32-36 36-40

Определите:

1) моду себестоимости продукции;

2) медиану себестоимости продукции.

3) Моду и медиану графически.

Задача 3.7. Определите относительные показатели вариации по данным о распределении посевной площади колхоза по урожайности пшеницы.

Урожайность пшеницы, ц/га	Посевная площадь, га
14-16 16-18 18-20 20-22 22-24

Задача 3.8. Имеются следующие распределения работников предприятия по стажу работы:

Стаж работы, лет	Численность работников
Мужчины	Женщины
Итого

Определите средний стаж работы: 1) мужчин; 2) женщин; 3) всех работников предприятия. Сделайте выводы.

Задача 3.9. Имеются следующие данные о продолжительности оплачиваемых отпусков работников, занятых на предприятиях региона:

Фактическая продолжительность отпуска, рабочих дней	Численность работников, в % к итогу
Итого: 100

Определите среднюю фактическую продолжительность отпуска по предприятиям региона.

Задача 3.10. Имеются следующие данные о товарообороте и издержках обращения торговых предприятий:

Издержки обращения на 100 руб. товарооборота, руб.	Число предприятий	Товарооборот в среднем на одно предприятие, млн. руб.
До 3 3 – 4 4 – 5 5 – 6 6 и выше
Итого: 40 -

Определите:

1) средний уровень издержек обращения на 100 руб. товарооборота;

2) средний размер товарооборота на одно предприятие.

Задача 3.11. Имеются следующие данные о заработной плате и численности рабочих по двум предприятиям отрасли:

Номер предприятия	Базисный период	Отчетный период
Средняя списочная численность рабочих, чел.	Средняя месячная заработная плата, руб.	Фонд заработной платы, руб.	Средняя месячная заработная плата, руб.
			977 850 1 129 850

Определите среднюю заработную плату рабочих по двум предприятиям в базисном и отчетном периодах. Сравните данные. Укажите, какие виды средних необходимо применить в каждом случае.

Задача 3.12. Имеются следующие данные по двум предприятиям:

Номер предприятия	Март	Апрель
Численность рабочих, чел.	Средняя выработка продукции одним рабочим за месяц, руб.	Выработано продукции всего, тыс. руб.	Средняя выработка продукции одним рабочим за месяц, руб.
			977 850 1 129 850

Определите среднюю выработку продукции за месяц в расчете на одного рабочего по двум предприятиям: 1) в марте; 2) в апреле. Укажите, какие виды средних необходимо применять в каждом случае. Объясните, какие факторы повлияли на изменение средней выработки продукции.

Задача 3.13. Имеются следующие данные о распределении студентов по росту:

Рост, см.	Численность студентов
До 162 162-166 166-170 170-174 174-178 178-182 182 и более
Итого: 500

Определите моду и медиану роста студентов, в том числе графически.

Задача 3.14. Имеются следующие данные, характеризующие распределение численности безработных по полу и возрасту:

Возраст, лет	Число безработных, в % к итогу	В том числе
Мужчин, в % к итогу	Женщин, в % к итогу
15-19 20-24 25-29 30-49 50-54 55-59 60-72	13,8 16,8 11,9 43,4 5,6 5,1 3,6	11,8 18,6 12,4 46,2 5,3 4,9 3,8	15,3 14,9 11,4 43,7 6,0 5,3 3,4
Итого:

Определите для всех безработных, для мужчин и женщин:

1) средний возраст безработных;

2) медианный возраст безработных.

3) модальный возраст безработных.

Задача 3.15. Анализы зональности угля по проценту содержания золы показали следующее распределение:

Процент зональности	Число проб
9-11 11-13 13-15 15-17 17-19 19-21 21-23 23-25

Вычислить: абсолютные и относительные показатели вариации.

Задача 3.16. Качество продукции предприятия характеризуется следующими данными (за месяц):

Вид продукции	Базисный период	Отчетный период
Процент брака	Стоимость бракованной продукции, руб.	Процент брака	Количество бракованной продукции
А В С	1,3 0,9 2,4		1,5 1,1 1,8

Определите средний процент брака в целом по предприятию в каждом периоде. Сделайте выводы.

Задача 3.17. Распределение студентов одного из факультетов по возрасту характеризуется следующими данными:

Возраст студентов, лет									Всего
Число студентов

Вычислите: а) размах вариации; б) среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; д) относительные показатели вариации возраста студентов.

Задача 3.18. При определении влажности торфа было обследовано 100 проб. В результате получены следующие данные:

Влажность торфа, (%)	Число проб
До 22 22-24 24-26 26-28 28-30 30-32 32 и выше

Вычислить: абсолютные и относительные показатели вариации.

Задача 3.19. Имеются следующие распределения работников предприятия по стажу работы:

Стаж работы, лет	Численность работников
Мужчины	Женщины
Итого

Вычислить: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации по численности мужчин и по численности женщин. Сравнить и сделать выводы.

Задача 3.20. Определите среднюю длину пробега автофургона торгово-посреднической фирмы и вычислите все показатели вариации, если известны:

Длина пробега за один рейс, км.	Число рейсов за квартал
30-50 50-70 70-90 90-110 110-130 130-150
Всего

Задача 3.21. Акционерные общества области по среднесписочной численности работающих на 1 января г. распределялись следующим образом:

Группы АО по средне-списочной числен-ности работаю-щих	до 400	400-600	600-800	800-1000	1000-1200	1200-1400	1400-1600	1600-1800	Ито-го
Количество АО

Рассчитайте: а) среднее линейное отклонение; б) дисперсию; в) среднее квадратическое отклонение; г) коэффициент вариации.

Задача 3.22. Работники по стажу работы распределяются следующим образом:

Стаж работы, лет	1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 5 16
Число рабочих	40 25 20 20 25 30 35 40 45 50 55 50 45 40 35 35

Вычислить: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Раздел 4. Ряды динамики.

Дата добавления: 2015-08-20