Править] Доказательство

Вывод одномерного уравнения Эйлера — Лагранжа является одним из классических доказательств в математике. Оно основывается на основной леммевариационного исчисления.

Мы хотим найти такую функцию , которая удовлетворяет граничным условиям , 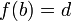и доставляет экстремум функционалу

Предположим, что имеет непрерывные первые производные. Достаточно и более слабых условий, но доказательство для общего случая более сложно.

Если даёт экстремум функционалу и удовлетворяет граничным условиям, то любое слабое возмущение , которое сохраняет граничные условия, должно увеличивать значение (если минимизирует его) или уменьшать (если максимизирует).

Пусть — любая дифференцируемая функция, удовлетворяющая условию . Определим

Поскольку даёт экстремум для , то , то есть

Интегрируя по частям второе слагаемое, находим, что

Используя граничные условия на , получим

Отсюда, так как — любая, следует уравнение Эйлера — Лагранжа:

Дата добавления: 2015-08-20