Доказательство

Квадрат касательной равен произведению секущей на её внешнюю часть.

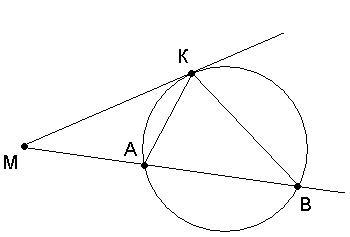
Теорема о квадрате касательной

Доказательство: Проведём отрезки АК и ВК (см. рисунок). Треугольники АКМ и ВКМ подобны: угол М у них общий, а углы АКМ и В равны, так как каждый из них измеряется половиной дуги АК. Следовательно, MK/MA = MB/MK, или MK² = MA·MB.

Теорема доказана.

Задача

Пусть Е и F - общие точки двух неравных пересекающихся окружностей, АD и BC - общие внешние касательные этих окружностей (А, В, С и D - точки касания, первые две - на одной окружности, остальные - на второй).

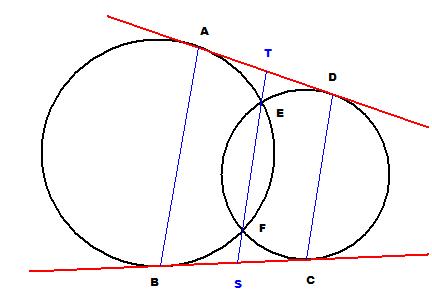
Пусть T - пересечение прямых AD и EF, а S - пересечение BC и EF. Доказать, что TS - средняя линия трапеции ABCD.

Доказательство

Для точки S: SB - касательная, а SFE - секущая. По теореме о касательной и секущей имеем SB²=SE*SF.
Опять же для точки S, но другой окружности: SC - касательная, а SFE - секущая. По теореме о касательной и секущей имеем SC²=SE*SF.
Тогда SB²=SC², откуда SB=SC.
По тем же причинам TA=TD.

Тогда T - средняя точка отрезка AD, а S - средняя точка отрезка BC. По определению, TS - медиана (средняя линия) трапеции ABCD. Средняя линия трапеции имеет следущие свойства: она делит высоту трапеции пополам, она параллельна двум основаниям (AB и CD), и её длина - половина суммы длин оснований: TS=(AB+CD)/2

Дата добавления: 2015-08-17