Частная корреляция больше чем трех величин

5. В соответствии с общей концепцией мы рассуждаем следующим образом.

Пусть имеется p -мерное невырожденное нормальное распределение, фиксируем p -2 случайных величины, то получаем частную корреляцию оставшихся двух (скажем, x ₁ и x ₂):

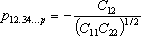, (6)

где C_ij - алгебраическое дополнение для p_ij в определителе

. (7)

Подобно (5), (6) следует рассматривать как общее определение частного коэффициента корреляции между x ₁ и x ₂ при фиксированных x ₃,..., x_p.

6. Полезно рассмотреть ту же задачу с другой точки зрения. Обозначим f (x ₁,..., x_k | x_k +1,..., x_p) условную совместную плотность распределения величин x ₁,..., x_k, когда x_k +1,..., x_p фиксированы, а g (x_k +1,..., x_p) - совместное маргинальное распределение x_k +1,..., x_p.

Совместная х. ф. всех p величин есть

,

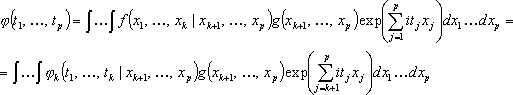где 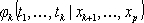- условная совместная х. ф. для x ₁,..., x_k. Из многомерной теоремы обращения следует, что

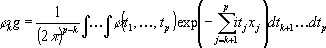. (8)

Если в (8) положить t ₁= t ₂=...= t_k =0, то из равенства 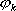единице получаем

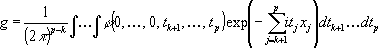. (9)

Следовательно, после деления (8) на (9) находим

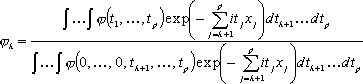. (10)

Этот общий результат вытекает из теоремы Барлетта (1938).

Предположим теперь, что наши p величин имеют многомерное нормальное распределение. Тогда, используя их х. ф., преобразуем подынтегральную функцию числителя в (10):

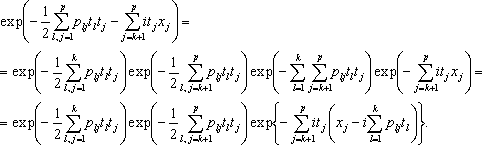(11)

Теперь интеграл относительно t_k +1,..., t_p от двух последних множителей в правой части (11) является обратным преобразованием многомерной нормальной х. ф. величин x_k +1,..., x_p, причем x_j отсчитывается от значения 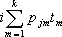. Это изменение начал координат не влияет на корреляции. Если обозначить D корреляционную матрицу величин x_k +1,..., x_p, то с точностью до постоянного множителя интеграл от (11) будет равен

.

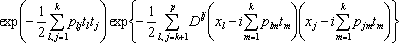Учитывая сказанное, из (10) имеем

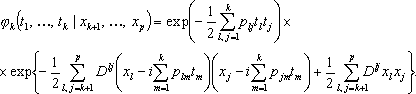(12)

Таким образом, если 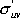обозначает ковариацию между x_u и x_v в условном распределении величин x ₁,..., x_k, а 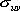- их безусловную ковариацию, то, сравнивая в (12) коэффициенты при t_u и t_v находим

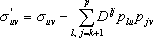. (13)

Это выражение получено в предположении, что исходные величины нормированы. Если теперь отказаться от нормировки, так что x_i будет иметь дисперсию 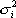, то каждое p заменится на соответствующие ему, 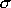, D^lj - на 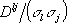, и мы получим более общую формулу соотношения (13):

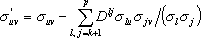. (14)

Равенство (14) не зависит от фиксируемых значений x_k +1,..., x_p.

Если обозначить безусловную (k × k)-матрицу рассеяния { 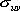} через A, (k ×(p - k))-матрицу { 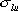} через B' и ((p - k)×(p - k))- матрицу рассеяния, из которой D получается в результате нормировки, через E, то (14) утверждает, что условная матрица рассеяния равна

.

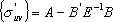7. В частности, если зафиксировать только одну переменную, скажем x_p, то D_pp =1, и условная ковариация (14) тогда равна

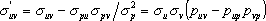. (15)

При u = v из (15) находим условную дисперсию u:

.

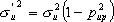Из двух последних формул получаем условный коэффициент корреляции того же вида, что и (5):

.

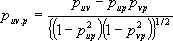Если зафиксируем все переменные, кроме двух, скажем x ₁ и x ₂, то из (14) будем иметь

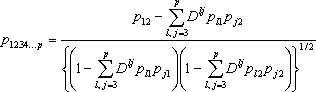. (16)

Рассматривая (7), находим, что минор элемента p ₁₂, а именно

,

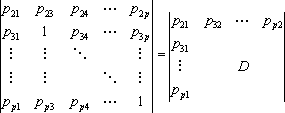может быть разложен по его первой строке и столбцу в виде

,

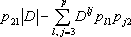и аналогично для миноров элементов p ₁₁, p ₂₂. Таким образом, (16) представимо в форме

,

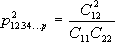что вновь совпадает с (6).

Анализ Дисперсионный (anova)

социологический словарь

- статистический метод, предназначенный для исследования причинной связи между переменной зависимой и одной или несколькими независимыми переменными (факторами). По числу независимых переменных, различают однофакторный А.Д., двухфакторный А.Д. и т.д. (не путать с Анализом факторным!) Зависимая переменная может быть только количественной, в то время как независимые переменные могут быть представлены номинальными, порядковыми или количественными шкалами (последние должны быть дискретными или сгруппироваными в интервалы). Первоначально А.Д. был разработан для обработки данных, полученных в ходе специально поставленных экспериментов, и считался единственным методом, корректно исследующим причинные связи. Однако в последние годы, вследствие общей либерализации взглядов на природу статистического анализа, он применяется также к данным, собранным в результате выборочных обследований, если численность выделяемых групп не слишком велика. В основе метода лежит сравнение средних значений зависимой переменной для групп, образованных комбинациями факторов (сами значения факторов не рассматриваются). Это обстоятельство позволяет некоторым авторам рассматривать А.Д. как обобщение t-критерия Стьюдента, предназначенного для сравнения средних значений переменной в двух группах. В А.Д. все различия в значениях зависимой переменной (y) объясняются двумя причинами: ее "собственной" или "естественной" изменчивостью, а также изменчивостью, вызванной влиянием независимых переменных, которые в данном случае называются факторами (Дисперсия объясненная). Соответственно сумма квадратов зависимой переменной SSобщая = (yij - y)2, где j - номер группы, к которой принадлежит объект с номером i, может быть разложена на две составляющие, одна из которых отражает собственную изменчивость y, а вторая - изменчивость, вызванную влиянием факторов: SSобщая = SSвнутригрупповая SSмежгрупповая. Модель однофакторного А.Д. предполагает, что среднее значение зависимой переменной y в группе с номером j (yj) зависит, во-первых, от среднего значения y по всей совокупности и, во-вторых, от эффекта j-го значения фактора xj, который обозначается альфаj: yj = y альфаj. Если фактор x не влияет на зависимую переменную y, то все альфаj = 0 и, следовательно, все yj = y, т.е. не отличаются друг от друга. Проверка гипотезы о влиянии фактора на зависимую переменную сводится к проверке нулевой гипотезы о том, что все альфаj равны нулю (H0: альфаj = 0 для всех значений j), означающей также, что все групповые средние равны друг другу, против альтернативной гипотезы, состоящей в том, что хотя бы для некоторых значений фактора xj эффекты альфаj отличны от нуля (H1: альфаj не равно 0 хотя бы для некоторых j). Принятие нулевой гипотезы означает признание независимости переменной y от фактора x; ее отклонение (и, соответственно, принятие альтернативной гипотезы) может служить подтверждением исследуемой причинной зависимости. Результаты однофакторного А.Д. представляются в виде стандартной таблицы, известной как таблица А.Д. (Таблицу 1 Приложения.) Если H0 верна, то F-отношение имеет распределение Фишера с dfмгр = k - 1 и dfвнгр = n - k степенями свободы. Нулевая гипотеза должна быть отклонена, если вычисленное значение F превысит критическое значение F1-альфа, где альфа - заданный уровень значимости. Многофакторный А.Д. концептуально не отличается от однофакторного. В двух- и многофакторных моделях проверяется ряд гипотез о влиянии на зависимую переменную каждого отдельно взятого фактора, а также их всевозможных сочетаний, что математически выражается в гипотезах о равенстве нулю прямых эффектов факторов и эффектов их взаимодействия. Для проверки таких гипотез межгрупповая сумма квадратов (SSмежгрупповая), представляющая вариацию зависимой переменной под общим влиянием всех факторов, делится на более мелкие составляющие, каждая из которых представляет прямой эффект одного из факторов или один из эффектов взаимодействия. А.Д. не позволяет судить о том, как именно влияют факторы на значение зависимой переменной, т.е. в каких конкретно группах средние достоверно различаются. Для проверки конкретных гипотез о характере таких различий используются метод парных сравнений и методы множественных сравнений. О.В. Терещенко

Источник: http://mirslovarei.com/content_soc/analiz-dispersionnyj-anova-11403.html#ixzz2T6M6SToY

Статистическая гипотеза является утверждением об неизвестном параметре, который формулируется в терминах математической статистики.

При проверке статистических гипотез используют два понятия: Н1 (гипотеза о различии) и Н0 (гипотеза о тождественности).

Итак, научная гипотеза используется для организации эксперимента, а статистическая - для организации процедуры сравнения параметров, измеряемых в эксперименте.

Вывод: теорию невозможно непосредственно проверить экспериментально. Теоретические утверждения являются универсальными. На их основе формулируют конкретные выводы (предположение), которые и являются гипотезами.

Научные гипотезы делятся на теоретические и эмпирические. Теоретические гипотезы выдвигают для преодоления внутренних противоречий в теории или для устранения несогласованности (разногласия) между теорией и экспериментальными данными.

Эмпирические гипотезы - это предположение, предпринимаемые для решения проблемы методом экспериментального исследования. Они не обязательно должны основываться на теории.

Основная особенность любой экспериментальной гипотезы заключается в том, что она должна быть операционализирована (т.е. сформулирована в терминах конкретной экспериментальной процедуры).

По содержанию выделяют следующие гипотезы:

1. О наличии явления (А);

2. О связи между явлениями (Б);

3. О предопределенности одного явления другим (В).

Примеры гипотез:

Тип А: В какой степени ограниченное количество символов, которые человек способна хранить в кратковременной памяти?

Тип Б: Можно интровертов считать осторожнее за экстра вертел?

Тип В: обусловлен интеллект детей интеллектом родителей?

Научная гипотеза должна отвечать критерию верификованости (т.е. способности быть подтвержденной или опровергнутой экспериментально).

"Добрые" гипотезы должны отвечать определенным критериям, то есть быть:

1. Логически связанными с существующими знаниями;

2. Содержательными, то есть содержать формулировку специфического связи между двумя основными понятиями;

3. Такими, позволяющих операционализации (т.е. трансформацию в совокупности переменных, которые можно измерять.

Дата добавления: 2015-08-20