Частная корреляция трех величин

3. Вначале естественно рассмотреть три величины, имеющие трехмерное нормальное распределение и в этом простейшем случае выписать формулу для вычисления частных корреляций, т.е. корреляции пары переменных при фиксированном значении третьей.

Исключим вырожденный случай и без потери общности, поскольку мы касаемся лишь корреляций, будем считать величины нормированными.

Тогда их матрица рассеяния совпадает с матрицей их корреляций, которую назовем корреляционной матрицей и обозначим C. Таким образом, если корреляция между x_i и x_j есть p_ij, то функция плотности распределения этих трех величин имеет вид

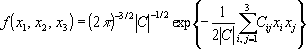, (1)

где C_ij - алгебраическое дополнение (i, j)-го элемента в симметричном корреляционном определителе

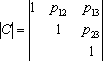. (2)

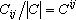есть элемент матрицы, обратной к C. Мы будем иногда записывать определитель или матрицу корреляций в таком виде, когда оставлено свободным место ниже главной диагонали, которое должно заполняться по симметрии.

Находим характеристическую функцию (х. ф.) этого распределения

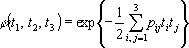. (3)

4. Рассмотрим корреляцию между x ₁ и x ₂ при фиксированном значении x ₃. Условное распределение x ₁ и x ₂ при заданном x ₃ равно

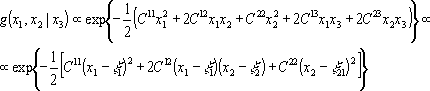, (4)

где .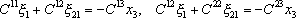

Из (4) видно, что при заданном x ₃ величины x ₁ и x ₂ имеют двумерное нормальное распределение с коэффициентом корреляции

.

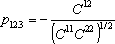Ясно, что p _12.3 не зависит от фиксируемого значения величины x ₃. Кроме того, сокращая на общий множитель | C | из (2) находим

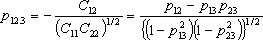. (5)

p _12.3 называется частным коэффициентом корреляции между x ₁ и x ₂ при фиксированном x ₃. Он симметричен относительно первичных индексов 1, 2. Его вторичный индекс 3 относится к переменной, которая фиксирована.

Хотя (5) выведено в предположении нормальности, мы теперь для любого исходного распределения определим частный коэффициент корреляции с помощью (5). Итак, по определению, для величин, отличных от нормальных, частная корреляция также вычисляется по формуле (5).

Рассмотрим теперь общий случай.

Дата добавления: 2015-08-20