ЗАДАЧА 4

ПРИМЕНЕНИЕ КЛАССИЧЕСКОГО МЕТОДА

ПРИ РАСЧЕТЕ ПЕРЕХОДНЫХ РЕЖИМОВ ЛИНЕЙНЫХ ЦЕПЕЙ

С ИСТОЧНИКАМИ ПОСТОЯННЫХ ЭДС

1. Исходные данные

Схема имеет три ветви: № 1, 2 и 3.

1.1. Ветвь 1 содержит элементы R, L, ветвь 2 - элемент С, ветвь 3 - элементы R, R ₁. Источник постоянной ЭДС произвольного направления включен в ветвь 1 при нечетном значении d, или в ветвь 3 - при четном значении d.

1.2. Коммутация осуществляется в зависимости от значений букв a, c кода таблицы 10.

Таблица 10

а	с	Описание коммутации
		Имеется ключ К, переключающий цепь с питания от источника Е на питание от источника Е 1 = 2 Е, где Е 1 совпадает по направлению с Е, Е 1 противоположно по направлению Е
		Элемент R 1 шунтирован ключом К: нормально замкнутым нормально разомкнутым
		Имеется нормально разомкнутый ключ: в ветви 2, в ветви 3
		Элемент R в ветви 1 шунтирован ключом К: нормально замкнутым нормально разомкнутым
		Нормально замкнутый ключ К шунтирует: элемент С, элемент R 1
		Имеется нормально разомкнутый ключ К: в ветви 1, в ветви 2

1.3. ЭДС Е = 10 е В, сопротивления R = 10 bf Ом, R ₁ = 90 bf Ом, индуктивность L = 1,25 d мГн, емкость С = 1,0 d мкФ.

2. Задание

2.1. Начертить схему согласно исходным данным (п.1).

2.2. Составить систему уравнений по законам Кирхгофа для определения неизвестных токов.

2.3. Определить закон изменения тока в ветви | c - d |, применив классический метод расчета.

2.4. Построить осциллограмму найденного тока для интервала времени 0 < t < 4/ç D ç, где D - меньший по модулю корень характеристического уравнения, если корни вещественные, или действительная часть одного из корней, если корни комплексно - сопряженные.

Классический метод расчета переходного режима

Исходные данные

Составляем схему электрической цепи и рассчитываем её элементы в соответствии с условием задачи и сформированным кодом (рис.1):

a	b	c	d	e	f

E = 10·e = 10·3 = 30 B

R = 10·b·f = 10·2·4 = 80 Ом

R₁ = 90·b·f = 90·2·4 = 720 Ом

L = 1.25·d = 1.25·1 = 0,001 мГн = 1,25E-3 Гн

С = 1,0·d = 1.0·1 = 1 мкФ = 1E-6 Ф

Задание

1.Определить закон изменения тока в ветви | c - d | = | 2 - 1 | = 1, применив классический метод расчета.

2.Построить график найденного тока.

В схеме цепи рис.1 в момент t = 0 мгновенно осуществляется коммутация. Определить закон изменения тока i₁ (t).

Решая эти уравнения получим:

Принужденное значение тока

Выражение для свободной составляющей определяется корнями характеристического уравнения

Начальные условия:

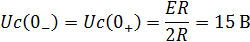
Ток в первой ветви:

Дата добавления: 2015-08-02