Основные определения теории систем массового обслуживания

Как было показано выше, основными составляющими частями модели телекоммуникационной системы с точки зрения теории телетрафика являются: поток требований на обслуживание, серверы, осуществляющие это обслуживание, и очередь из требований, ожидающих обслуживания. Эта модель полностью соответствует более широкой по своим приложениям и глубоко математичной по подходу теории систем массового обслуживания. Эта теория рассматривает процессы обслуживания не только относящиеся к передаче и обработке информации, а любые задачи, которые могут быть сведены к приведенной выше модели. Это может быть, например, обслуживание клиентов в парикмахерской. В роли серверов здесь выступают мастера-парикмахеры, клиенты могут рассматриваться как поступающие требования, а очередь требований отождествляется с клиентами в зале ожидания. Другими задачами теории массового обслуживания являются известная проблема обработки однотипных деталей группой станков или перевозки грузов несколькими транспортными средствами.

Основной количественной характеристикой, описывающей функционирование системы массового обслуживания, является выполненная ею работа за некоторый интервал времени. Определим величину работы U, выполненной системой массового обслуживания за интервал времени Т, как суммарное время, затраченное на обслуживание требований в этой системе всеми входящими в нее серверами в течение этого интервала. Обозначим выполненную работу как

.

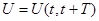Для системы, содержащей один сервер, максимальная работа, которая может быть выполнена за время T, равна 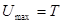. Если система содержит n серверов, то за это время может быть выполнена работа .

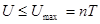В практической телефонии работу часто измеряют величиной, называемой часозанятием, т.е. измеряют работу СМО в часах. Мы будем пользоваться также термином секундозанятие, чтобы не путать величину выполненной работы и времени, за которое эта работа была выполнена.

Рассмотрим, как может быть определена работа, выполненная системой, содержащей, например, три сервера, занятых обслуживанием поступающих требований в соответствие с временной диаграммой, представленной на рис.1.1.

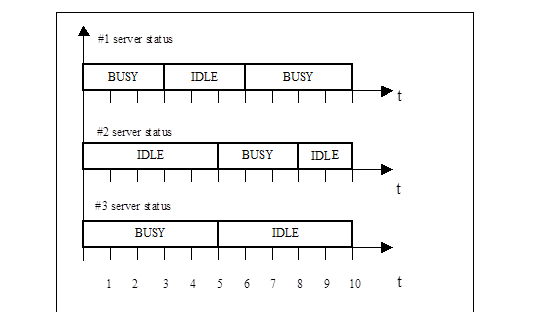Рис. 1.1. Временная диаграмма СМО из трех серверов.

Первые три интервала времени (будем считать каждый из них для определенности секундой), заняты первый и третий сервер, следующие два интервала – только третий, затем одну секунду работает только второй, потом, две секунды второй и первый, и последние две секунды работает только первый. Поэтому нетрудно записать

.

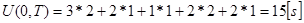Значит в рассмотренном случае работа, выполненная тремя серверами за 10 секунд равна 15 секундозанятиям. Заметьте сразу, что максимальная работа, которая могла бы быть выполнена ими за это время, равна 30 секундозанятий.

Понятие работы характеризует степень занятости (загрузку) серверов только совместно с указанием интервала времени, за который эта работа была выполнена. В большинстве практических случаев используется производная от работы, называемая мгновенной нагрузкой:

,

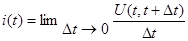Для каждого сервера работа 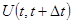равна нулю, если в интервал 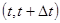сервер не занят, и равна 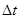, если сервер занят, поэтому, стоящее под знаком предела отношение равно 0 или 1. Значит для системы из n серверов физический смысл мгновенной нагрузки - это число серверов, занятых обслуживанием в данный момент времени. Поскольку мгновенная нагрузка величина случайная, то обычно используется ее математическое ожидание:

,

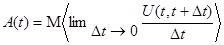называемое интенсивностью нагрузки (traffic intensity), т.е. среднее число серверов, занятых в данный момент времени.

Символ «М<>» обозначает здесь и далее математическое ожидание случайной величины.

На практике, интенсивность нагрузки оценивается на конечном интервале 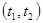. При этом полагают:

.

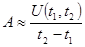Единицей измерения интенсивности нагрузки является один Эрланг (1 Эрл). Из определения интенсивности нагрузки ясно, что 1 Эрланг – это интенсивность нагрузки, которая требует полной занятости СМО с одним сервером или интенсивность, при которой одним сервером выполняется работа величиной в одно секундозанятие за время в 1 секунду. В практической телефонии говорят об интенсивности нагрузки в 1 Эрланг как об интенсивности, определяющей одно часозанятие в час.

Вернемся к приведенному выше примеру СМО с тремя серверами, функционирование которой определено диаграммой на Рис.1.1.

Приведенная выше формула позволяет рассчитать мгновенную нагрузку в момент времени t = 1 как i (1)=1+1=2 Эрланга, i (9)=1. Оценить интенсивность нагрузки можно, рассматривая работу на конечных интервалах времени. Если рассмотреть первые 5 секунд, то выполненная работа будет равна 8 секундозанятиям, а за последние 5 секунд – 7 секундозанятий, и интенсивность нагрузки в первой половине рассматриваемого интервала будет оцениваться величиной 8/5=1.6 Эрланга, а во второй половине – 7/5=1,4 Эрланга. Следовательно, величина интенсивности нагрузки носит локальный характер и позволяет описывать динамику, то есть изменения нагрузки в течение времени. Рассмотренная СМО, например, первые пять секунд работала более интенсивно, чем последующие пять. Более того, мы можем количественно сравнить эти изменения.

В практической телефонии в соответствие с рекомендацией ITU E.500 интенсивность нагрузки оценивается на интервалах длительностью в 15 минут и определяется средняя нагрузка в течение часа, в пределах которого эта нагрузка была максимальной. Обычно интервал времени длиной в час, интенсивность нагрузки, в течение которого бывает максимальной, повторяется каждые сутки, например с 11 до 12 часов. Такой интервал принято называть часом наибольшей нагрузки (ЧНН).

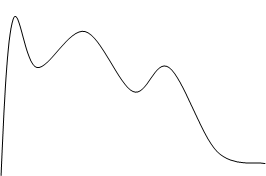
Рекомендация ITU E.500 определяет нагрузку в фиксированный ЧНН как среднее значение за 30 наиболее загруженных дней 12-месячного периода (нормальная интенсивность нагрузки ЧНН, или уровень А) и за 5 самых нагруженных дней 30-дневного периода (повышенная интенсивность или уровень В). На рисунке 1.2 приведены результаты измерения интенсивности нагрузки на нескольких городских АТС. Как видно из рисунков час наибольшей нагрузки может быть различным на различных АТС.

Эрл

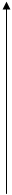120

Час

Рис.1.2. Результаты измерения интенсивности нагрузки на нескольких городских АТС.

В американской литературе вы можете встретить и другую единицу измерения интенсивности нагрузки, называемую CCS – Centrum (or hundred) calls second (гектосекундозанятия). Это число отражает работу серверов в сто секундных единиц измерения в течение часа.

Вы всегда можете пересчитать CCS в Эрланги по формуле

36 CCS=1 Эрланга

Всюду выше мы говорили о реально измеренной нагрузке, которая соответствует совершенной СМО работе. Такая нагрузка называется обычно обслуженной нагрузкой. Если часть поступивших требований не была обслужена системой ввиду перегрузки серверов, то можно ввести понятия потенциальной нагрузки и поступающей нагрузки. Потенциальная нагрузка – это гипотетическая обслуженная СМО нагрузка в предположении, что все требования были обслужены. Поступающая нагрузка определяется как произведение среднего числа поступающих требований в единицу времени на среднее время одного обслуживания. Разность между потенциальной и обслуженной нагрузкой называют потерянной, а разность между поступающей и обслуженной – избыточной нагрузкой.

Ненулевое значение потерянной или избыточной нагрузки говорит о ненулевой вероятности блокировки или пропуска требований или ненулевом значении задержки требований во входной очереди. Как было уже отмечено выше, значения вероятности блокировки или пропуска, а также параметры функции распределения задержки, чаще всего среднее значение задержки, определяют так называемые показатели качества обслуживания (QoS-Quality of Service).

Важными характеристиками системы массового обслуживания являются ее производительность и пропускная способность.

Пропускная способность системы - это интенсивность обслуженной нагрузки при заданном качестве обслуживания.

Производительность системы - это предельное, статистически усредненное число обслуживаний в единицу времени при заданном качестве обслуживания.

Дата добавления: 2015-08-02