Прямая в пространстве и плоскость

53. Установите соответствие

1) Параметрические уравнения прямой в пространстве

2) Уравнения прямой, проходящей через две данные точки в пространстве

3) Общее уравнение прямой в пространстве

4) Канонические уравнения прямой в пространстве

a)

b)

c)

d)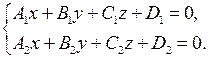

54. Каноническое уравнение прямой в пространстве имеет вид

a)

b)

c)

d)

55. Уравнение прямой в пространстве, принадлежащей двум плоскостям имеет вид

a)

b)

c)

d)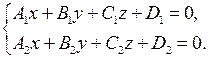

56. Параметрические уравнения прямой в пространстве имеют вид:

a)

b)

c)

d)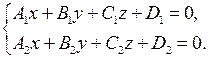

57. Уравнение прямой в пространстве, проходящее через две заданные точки имеет вид

a)

b)

c)

d)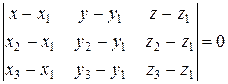

58. Если прямая в пространстве задана в виде 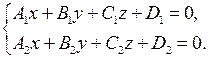, то чтобы найти ее направляющий вектор, необходимо вычислить:

a) , т.е. разность векторов и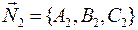

b) , т.е. векторное произведение векторов и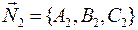

c) , т.е. сумму векторов и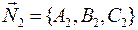

d) , т.е. скалярное произведение векторов и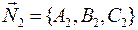

59. Угол между двумя прямыми в пространстве 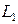с направляющим вектором и с направляющим вектором вычисляется по формуле:

a)

b)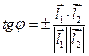

c)

d)

60. Пусть прямая в пространстве 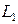имеет направляющий вектор , - направляющий вектор . Тогда условие является условием ………………………. двух прямых:

a) параллельности

b) перпендикулярности

c) пересечения

d) совпадения

61. Пусть прямая в пространстве 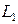имеет направляющий вектор , - направляющий вектор . Тогда условие является условием ………………………. двух прямых:

a) параллельности

b) перпендикулярности

c) пересечения

d) совпадения

62. Условие пересечения двух прямых в пространстве 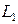с направляющим вектором и с направляющим вектором имеет вид:

a)

b)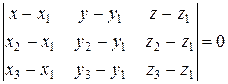

c)

d)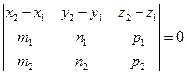

63. Угол между прямой с направляющим вектором 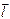и плоскостью в пространстве вычисляется по формуле:

a)

b)

c)

d)

64. Пусть прямая в пространстве имеет направляющий вектор 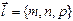, плоскость имеет вид . Тогда условие является условием:

a) параллельности прямой и плоскости

b) перпендикулярности прямой и плоскости

c) принадлежности прямой плоскости

65. Пусть прямая в пространстве имеет направляющий вектор 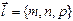, плоскость имеет вид . Тогда условие 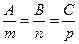является условием:

a) параллельности прямой и плоскости

b) перпендикулярности прямой и плоскости

c) принадлежности прямой плоскости

66. Установите соответствие:

1) Угол между прямыми на плоскости

2) Угол между прямыми в пространстве

3) Угол межу плоскостями

4) Угол между прямой и плоскостью

a)

b)

c)

d)

67. Установите соответствие:

1) Общее уравнение прямой на плоскости

2) Общее уравнение плоскости

3) Каноническое уравнение прямой в пространстве

4) Уравнение плоскости в отрезках

a)

b) Ax +Ву +С = 0

c) Ах+By+Cz+D=0

d)

68. Установите соответствие:

1) Условие параллельности прямых на плоскости

2) Условие параллельности плоскостей

3) Условие параллельности прямой и плоскости в пространстве

4) Условие параллельности прямых в пространстве

_a) k₁ = k₂

_b)

c)

d)

69. Установите соответствие:

1) Условие перпендикулярности прямых на плоскости

2) Условие перпендикулярности плоскостей

3) Условие перпендикулярности прямой и плоскости в пространстве

4) Условие перпендикулярности прямых в пространстве

a)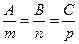

b) k₁k₂ = -1

c)

d)

70. Установите соответствие:

1) Нормальный вектор плоскости

2) Расстояние от точки М до плоскости

3) Направляющий вектор прямой в пространстве

4) Расстояние от точки М до прямой на плоскости

a)

b)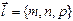

c)

d)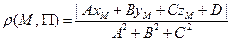

---

Дата добавления: 2015-08-02