
Читайте также:
|
1) **Плотность неизвестного газа r=0,09 кг/м3. При этом в объёме V=0,1 м3 содержится N=2,7 · 1024 молекул. Рассчитав молярную массу газа, определите, какой это газ.
Дано: r=0,09 кг/м3,
V=0,1 м3,
N=2,7×1024;
M=?
Решение. Значение молярной массы газа получим, используя выражение для количества вещества:
n=  =
= 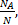 Þ М=m
Þ М=m 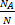
Масса газа т связана с занимаемым объемом и плотностью соотношением: m=rV. Окончательно получим:М=m 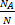 = rV
= rV 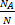 . Проведем вычисления: M=
. Проведем вычисления: M=  = 2×
= 2× 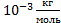
Наименьшая молярная масса у атомарного водорода Мн= 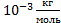 . Следовательно, неизвестный газ может содержать только два атома водорода. Это молекулярный водород Н2.
. Следовательно, неизвестный газ может содержать только два атома водорода. Это молекулярный водород Н2.
2) **В баллоне объёмом V=10 л находится газ при температуре t=27 oС. Вследствие утечки газа давление снизилось на Δр=4,2 кПа. Сколько молекул ΔN вышло из баллона?
Дано: V=0,01м3
Т= (27+273)К
Δр=4,2×103Па
ΔN=?
Решение: p=nkT =  k×T,Þ N =
k×T,Þ N = 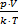 . Найдем первоначальное и конечное число молекул в баллоне: N1 =
. Найдем первоначальное и конечное число молекул в баллоне: N1 = 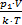 , N2 =
, N2 = 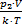 , тогда число молекул, покинувших баллон: DN=N2-N1=
, тогда число молекул, покинувших баллон: DN=N2-N1= 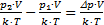 . Проведем вычисления: DN=
. Проведем вычисления: DN= 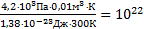
Ответ: из баллона вышло N= 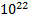 молекул.
молекул.
3) **При повышении температуры идеального газа на DT1=150 K средняя скорость движения его молекул увеличилась с υ1=400 м/с до υ2=500 м/с. На сколько еще нужно нагреть этот газ, чтобы увеличить среднюю скорость его молекул до υ3=600 м/с?
Дано: DT1=150 K
υ1=400 м/с
υ2=500 м/с
υ3=600 м/с
DТ2=?
Решение: p=nkT= 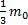 n
n 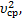 Þ Т=
Þ Т= 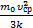 . Здесь k=1,38×10-23
. Здесь k=1,38×10-23 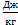 – постоянная Больцмана. Тогда Т1=
– постоянная Больцмана. Тогда Т1= 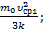 Т2=
Т2= 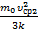 ; Т3=
; Т3= 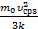 . Сейчас можно выразить изменение температуры согласно условия задачи DT1=Т2–Т1=
. Сейчас можно выразить изменение температуры согласно условия задачи DT1=Т2–Т1= 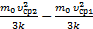 =
= 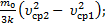 DТ2=Т3–Т2=
DТ2=Т3–Т2= 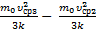 =
= 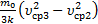 .
.
Разделим первое уравнение на второе: 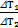 =
= 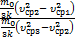 , Þ после сокращения получим DТ2=DT1×
, Þ после сокращения получим DТ2=DT1×  . Проведем вычисления: DТ2=150K×
. Проведем вычисления: DТ2=150K× 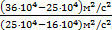 » 183,33K.
» 183,33K.
Ответ: DТ2=DT1×  =183,33 K
=183,33 K
4)
| V2, p2 |
| V1, p1 |
V1=240 × 10-9 м3
V2=200 × 10-9 м3
r=13600 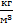
p0=?
Решение. Воздух, запертый столбиком ртути в трубке, имеет постоянную массу и температуру, значит, для него можно использовать закон Бойля-Мариотта: m, T=const, Þ pV=const. Выразим начальное и конечное давление воздуха в трубке: в горизонтальной трубке на столбик ртути слева и справа давления одинаковы, иначе столбик будет смещаться до тех пор, пока давления не выровняются p1=p0, здесь p0– атмосферное давление; когда трубка вертикальна, на воздух давят атмосфера и столбик ртути, значит, p2=p0+rgl
Итак, p1V1=p2V2 или p0V1=(p0+rgl)×V2. Раскроем скобки и выразим p0:
p0V1=p0V2+rgl×V2, Þ p0V1-p0V2=rgl×V2, Þ p0(V1-V2)=rgl×V2, Þ 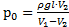 . Найдем это давление:
. Найдем это давление:
p0= 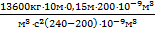 = 102×103Па
= 102×103Па
Ответ: p0= 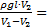 102кПа
102кПа
5) **В вертикальном цилиндрическом сосуде под подвижным поршнем находится 2 моля гелия и 1 моль молекулярного водорода. Температуру смеси увеличивают в два раза. При этом весь водород распадается на атомы. Во сколько раз увеличивается объем газа под поршнем?
Дано: 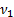 =2 моль
=2 моль
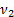 =1моль
=1моль
Т2=2Т1
 =?
=?
Решение. Для газов в сосуде используем уравнение Менделеева-Клапейронаp1V1=ν1RT1для гелия и p2V1=ν2RT1 для молекулярного водорода. Согласно закону Дальтона р=р1+р2= 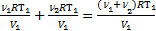 .
.
По условию задачи поршень подвижен, значит, при увеличении температуры смеси в начальный момент давление начнет увеличиваться, газ будет давить на поршень снизу, поднимая его до тех пор, пока давление смеси не станет равным первоначальному. Ведь на смесь давление сверху не меняется (давление атмосферы плюс давление самого поршня).
Так как H2 распался на атомы, то количество частиц увеличилось в 2 раза. Следовательно, количество вещества тоже увеличилось в 2 раза: 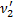 =2
=2 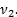 Для нагретой смеси по закону Дальтона аналогично: р=р¢1+р¢2=
Для нагретой смеси по закону Дальтона аналогично: р=р¢1+р¢2= 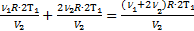 . Тогда можно приравнять правые части выражений для обоих давлений смеси:
. Тогда можно приравнять правые части выражений для обоих давлений смеси: 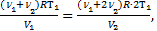 Þ
Þ 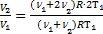 или
или 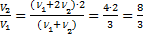 . Ответ:
. Ответ: 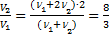
6) **Сосуд объемом V=20 л содержит смесь водорода и гелия при температуре t=20 °С и давлении p=2 атм. Масса смеси m=5 г. Найти отношение массы водорода к массе гелия в смеси.
Решение. Запишем уравнения состояния для водорода и гелия: р1V=(m1/M1)×RT и р2V=(m2/M2)×RT.
По закону Дальтона давление смеси газов равно сумме парциальных давлений этих газов в отдельности: р=р1+р2. И так как из уравнений состояния водорода и гелия для давлений имеем р1= 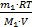 и р2=
и р2= 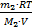 , то общее давление смеси газов: р=
, то общее давление смеси газов: р= 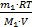 +
+ 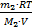 =
= 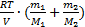 . Но т=т1+т2, тогда р=
. Но т=т1+т2, тогда р= 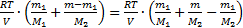 . Отсюда
. Отсюда 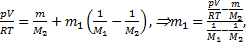
Þ 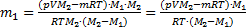 .
.
Далее находим т2, она равна т2=т-т1=m- 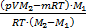 =
= 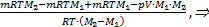
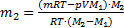 .
.
Теперь найдем отношение 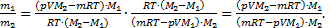 И выполним расчеты:
И выполним расчеты: 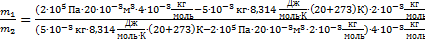 ,Þ
,Þ
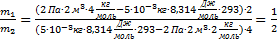 ∙
∙ 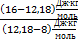 »0,458, Þ
»0,458, Þ 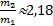
| V |
| Т |
| 2 |
| 3 |
| 1 |
| 0 |
| Рис. 4 |
| 4 |
7) **Изобразите на р-Т диаграмме процесс, проводимый с идеальным газом, приведенный на рисунке 4, если известно что в процессе изобарного нагревания температура газа увеличивается в п=3 раза.
| V |
| Т |
| 2 |
| 3 |
| 1 |
| 0 Т 3Т |
| Рис. 4, дополненный |
| 4 |
1) 1-2 - изохора, Þ V=const, р/T=const, тогдар ↓-сяиT ↓-ся;
2-3 - изобара, Þ р=const, V/T=const, тогдаT ↑-ся и V ↑-ся;
3-4 - изохора, Þ V=const, р/T=const, тогдаT ↑-сяир ↑-ся;
4-1 - изобара, Þ р=const, V/T=const, тогдаT ↓-ся иV ↓-ся.
| р |
| Т |
| 2 |
| 1 |
| 3 |
| 0 Т 3Т |
| Рисунок для ответа |
| 4 |
| р |
| 3р |
 2) Кроме того по условию известно, что в процессе изобарного нагревания температура газа увеличивается в п=3 раза. Учтем это:
2) Кроме того по условию известно, что в процессе изобарного нагревания температура газа увеличивается в п=3 раза. Учтем это:
2-3 – изобара, где температура увеличивается в 3 раза, р=const, => V2/V3=T2/T3=T2/3T2, =>V3=3V2, => T1=T3=3T2. Рисунок для ответа смотри справа.
8) 

 **Процесс, представленный на р-Т диаграмме (рис. 5), протекает при постоянном объёме газа. В каком состоянии 1, 2 или 3 газ имеет наибольшую массу?
**Процесс, представленный на р-Т диаграмме (рис. 5), протекает при постоянном объёме газа. В каком состоянии 1, 2 или 3 газ имеет наибольшую массу?
Решение. Согласно уравнению Менделеева-Клапейрона 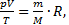 отсюда
отсюда 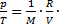 m. Если с учетом условия выражение
m. Если с учетом условия выражение 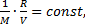 то отношение
то отношение  пропорционально массе газа:
пропорционально массе газа: 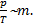 Но отношение
Но отношение  представляет собой тангенс угла наклона a линии,проходящей через «0» и точку 1 (2 или 3), описывающую состояние газа, занимающего постоянный объем. Из курса математики известно, что чем больше угол наклона, тем тангенс этого угла больше. По диаграмме очевидно, что a2>a3>a1, Þ tga2>tga3>tga1, Þ
представляет собой тангенс угла наклона a линии,проходящей через «0» и точку 1 (2 или 3), описывающую состояние газа, занимающего постоянный объем. Из курса математики известно, что чем больше угол наклона, тем тангенс этого угла больше. По диаграмме очевидно, что a2>a3>a1, Þ tga2>tga3>tga1, Þ 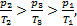 Þ m2>m3>m1.Итак, наибольшую массу m газ имеет в состоянии 2. Ответ: наибольшую массу m газ имеет в состоянии 2
Þ m2>m3>m1.Итак, наибольшую массу m газ имеет в состоянии 2. Ответ: наибольшую массу m газ имеет в состоянии 2
9)
| р |
| V |
| 2 |
| 3 |
| 1 |
| 0 |
| Рис. 6 |
| 4 |
Решение. Согласно графику процесса участки 2-3 и 4-1 – изотермы, тогда согласно закону Бойля-Мариоттаp2V2=p3V3(1) и p4V4=p1V1(2). Линии 1-2 и 4-3 проходят через «0», значит, на этих участках давление прямо пропорционально его объему p~V, т.е. 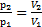 (3) и
(3) и 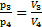 (4).
(4).

 Так как вопрос задачи касается объема, значит необходимо из уравнений 1-4 исключить давления. Это можно сделать самыми разными способами. Например, найдем p2 из уравнения (3):
Так как вопрос задачи касается объема, значит необходимо из уравнений 1-4 исключить давления. Это можно сделать самыми разными способами. Например, найдем p2 из уравнения (3): 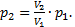 Аналогично, из уравнения (4) найдем p3:
Аналогично, из уравнения (4) найдем p3: 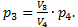 Подставим эти значения в уравнение (1):
Подставим эти значения в уравнение (1): 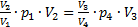 или
или 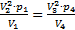 (*). Обратим внимание, что в уравнение (2) входят те же величины: p1V1=p4V4. (**) Разделим уравнение (*) на уравнение (**):
(*). Обратим внимание, что в уравнение (2) входят те же величины: p1V1=p4V4. (**) Разделим уравнение (*) на уравнение (**): 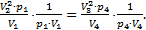 Отсюда после сокращения давлений получаем:
Отсюда после сокращения давлений получаем: 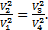 Извлекая корни из левой и правой частей равенства с учетом условия V2=V4, получим:
Извлекая корни из левой и правой частей равенства с учетом условия V2=V4, получим: 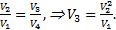 Ответ:
Ответ: 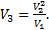
10)  ** Какое количество природного газа надо сжечь, чтобы m1=4 кг льда при t1=-10 oС обратить в пар с температурой t2=100 oС? КПД нагревателя η=60 %. Удельная теплота сгорания природного газа q=34 МДж/кг. Удельные теплота плавления льда λ=330 кДж/кг, теплота парообразования для воды L=2,25 МДж/кг и теплоемкость воды c=4200 Дж/(кг · К).
** Какое количество природного газа надо сжечь, чтобы m1=4 кг льда при t1=-10 oС обратить в пар с температурой t2=100 oС? КПД нагревателя η=60 %. Удельная теплота сгорания природного газа q=34 МДж/кг. Удельные теплота плавления льда λ=330 кДж/кг, теплота парообразования для воды L=2,25 МДж/кг и теплоемкость воды c=4200 Дж/(кг · К).
Решение. Согласно определению коэффициента полезного действия 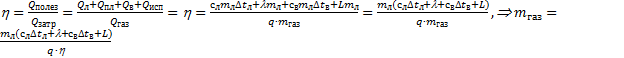 .
.
 Выполним расчеты:
Выполним расчеты: 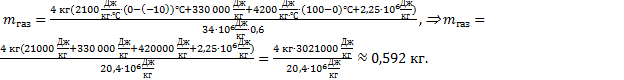
Ответ: 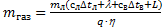 »0,592 кг.
»0,592 кг.
11) **В медный сосуд, нагретый до температуры t1=350 oС, положили m2=600 г льда при температуре t2=-10 oС. В результате в сосуде оказалось m3=550 г льда, смешанного с водой. Определить массу сосуда m1.
Решение. Согласно условию в сосуде оказались лед с водой, это значит, что конечная температура содержимого сосуда равна t=0°C. Используем уравнение теплового баланса для описанной ситуации: 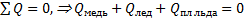 , Þ
, Þ 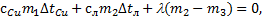 отсюда можно выразить массу сосуда m1:
отсюда можно выразить массу сосуда m1: 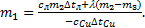 Выполним расчеты:
Выполним расчеты: 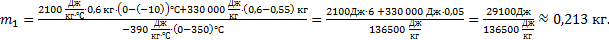
Ответ: 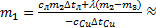 0,213 кг.
0,213 кг.
12) **На сколько изменится масса и внутренняя энергия воздуха в комнате при повышении температуры в ней от t1=10 oС до t2=50 oС? Давление p=105 Па. Объём воздуха в комнате V=100 м3.
Решение. 1) Согласно уравнению Менделеева-Клапейрона 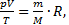 отсюда
отсюда 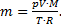 Тогда изменение массы воздуха при повышении температуры воздуха в комнате
Тогда изменение массы воздуха при повышении температуры воздуха в комнате 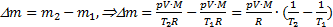 . Выполним расчеты:
. Выполним расчеты: 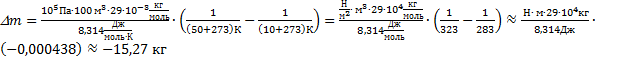 .
.
2) Чтобы определить, как изменится внутренняя энергия воздуха в комнате, используем формулу для внутренней энергии идеального газа: 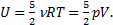 Учтем, что объем комнаты не меняется при нагревании воздуха, как и давление в ней, потому что оно всегда равно давлению внешнему, то есть V1=V2и р1=р2. Дело в том, что комната - не герметичная система, и нагрев получается изобарическим. Воздух при нагреве будет расширяться и уходить на улицу, унося тепло, полученное при нагревании. Итак,
Учтем, что объем комнаты не меняется при нагревании воздуха, как и давление в ней, потому что оно всегда равно давлению внешнему, то есть V1=V2и р1=р2. Дело в том, что комната - не герметичная система, и нагрев получается изобарическим. Воздух при нагреве будет расширяться и уходить на улицу, унося тепло, полученное при нагревании. Итак, 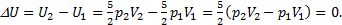
| р |
| V |
| 2 |
| 3 |
| 1 |
| 0 |
| Рис. 7 |
| р2 |
| р1 |
| V1= V2 V3 |
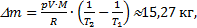 внутренняя энергия воздуха в комнате не изменилась
внутренняя энергия воздуха в комнате не изменилась 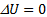 .
.
13) **Некоторая масса газа, занимающего объём V1=0,01 м3, находится под давлением p=1·105 Па при температуре T1=300 K. Газ нагревают при постоянном объёме до температуры T2=320 K, а затем при постоянном давлении до температуры T3=350 K. Найти работу, совершаемую газом при переходе из состояния 1 в состояние 3. (см. рис.7)
Решение. По графику зависимости давления от объема p(V) можно найти работу, совершаемую газом, как площадь фигуры под этим графиком p(V), ограниченной снизу осью объема.
Тогда А1-3=р2×(V3-V1). На участке 1-2 V1=V2, значит, газ работу не совершает. Согласно закону Шарля 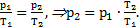 На участке 2-3 р2=р3, значит, по закону Гей-Люссака
На участке 2-3 р2=р3, значит, по закону Гей-Люссака 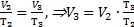 . Эти выражения для давления р2и объема V3 подставим в формулу для работы газа: А1-3=р2×(V3-V1)=
. Эти выражения для давления р2и объема V3 подставим в формулу для работы газа: А1-3=р2×(V3-V1)= 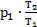 ×(
×( 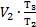 -V1), но V1=V2, тогда А1-3=
-V1), но V1=V2, тогда А1-3= 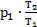 ×(
×( 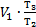 -V1)=
-V1)= 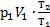 ×(
×( 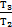 -1)=
-1)= 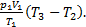 Выполним расчеты: А1-3=
Выполним расчеты: А1-3= 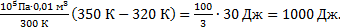
 Ответ: А1-3=
Ответ: А1-3= 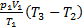 =1000 Дж.
=1000 Дж.
14)
| р |
| V |
| 2 |
| 3 |
| 1 |
| 0 |
| Рис. 8 |
Решение. По графику
Дата добавления: 2015-08-02; просмотров: 138 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЗАДАНИЕ 3 | | | Задачи для переводного экзамена |