|
Читайте также: |
Приклад. Знайти частинні похідні від функції 
.
.
Як бачимо, частинна похідна від функції двох змінних також є функцією двох змінних.
Тому її теж можна диференціювати за кожною із змінних. Результатом такого диференціювання є частинні похідні другого порядку:
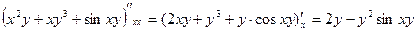
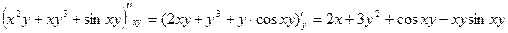
Позначення: 
; 
.
Означення. Частинна похідна довільного порядку, взята за різними змінними називається змішаною частинною похідною.
Теорема. Якщо функція 
має змішані неперервні частинні похідні другого порядку в деякій області, то вони співпадають в цій області: 
. (див. попередній приклад)
Приклад. Знайти другі частинні похідні 
:
1. 
| Розв’язування.  ;  ;
 ;  ;  ;  .
|
2. 
| Розв’язування.  ;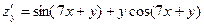 
 ; 
  ;
 .
|
Екстремум функції двох змінних
Означення 1. Точка М(х0, у0) називається точкою локального максимума функції двох змінних , якщо  , де  і  досить малі проміжки.
Означення 2. Точка P(х0, у0) називається точкою локального мінімума функції двох змінних , якщо  , де і досить малі проміжки.
|  z
•
y
М(х0, у0)
x
|
Теорема 1. Щоб функція мала екстремум у точці M(х0,у0), необхідне виконання двох умов:
, або не існує
, або не існує.
Точки з такими властивостями називаються стаціонарними точками функції двох змінних.
Дата добавления: 2015-08-02; просмотров: 122 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Частинні похідні | | | Достатні умови екстремумА |